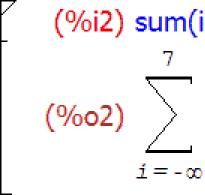Maxima опис. Методика роботи з maxima
Математичний пакет Maxima – одна з найкращих безкоштовних замін маткаду.
Даний навчальний посібник (у форматі pdf) може бути використаний в рамках дисциплін математичний аналіз, диференціальні рівняння, пакети прикладних програм та ін. рамках курсів на вибір. Воно також може бути корисним для знайомства із системами комп'ютерної математики у профільних класах загальноосвітніх установ із поглибленим вивченням математики та інформатики.
- Передмова
- Глава 1. Основи роботи у системі комп'ютерної математики Maxima
- 1.1. Про систему Maxima
- 1.2. Встановлення Maxima на персональний комп'ютер
- 1.3. Інтерфейс основного вікна Maxima
- 1.4. Робота з осередками в Maxima
- 1.5. Робота з довідковою системою Maxima
- 1.6. Функції та команди системи Maxima
- 1.7. Управління процесом обчислень у Maxima
- 1.8. Найпростіші перетворення виразів
- 1.9. Розв'язання алгебраїчних рівнянь та їх систем
- 1.10. Графічні можливості
- Глава 2. Чисельні методи розв'язання диференціальних рівнянь
- 2.1. Загальні відомості про диференціальні рівняння
- 2.2. Численні методи вирішення задачі Коші для звичайного диференціального рівняння першого порядку
- 2.2.1. Метод Ейлера
- 2.2.2. Метод Ейлера-Коші
- 2.2.3. Метод Рунге-Кутта 4 порядку точності
- 2.3. Вирішення крайових завдань для звичайних диференціальних рівнянь шляхом кінцевих різниць
- 2.4. Метод сіток для вирішення диференціальних рівнянь у приватних похідних
- Глава 3. Знаходження рішень диференціальних рівнянь у системі Maxima
- 3.1. Вбудовані функції знаходження рішень диференціальних рівнянь
- 3.2. Розв'язання диференціальних рівнянь та їх систем у символьному вигляді
- 3.3. Побудова траєкторій та поля напрямів диференціальних рівнянь.
- 3.4. Реалізація чисельних методів розв'язання задачі Коші для звичайних диференціальних рівнянь
- 3.4.1. Метод Ейлера
- 3.4.2. Метод Ейлера-Коші
- 3.4.3. Метод Рунге-Кутта
- 3.5. Реалізація звичайно різницевого методу вирішення крайової задачі для звичайних диференціальних рівнянь
- 3.6. Реалізація методу сіток для диференціальних рівнянь у приватних похідних
- Завдання для самостійного вирішення
- Література
Передмова
Теорія диференціальних рівнянь одна із найбільших розділів сучасної математики. Однією з основних особливостей диференціальних рівнянь є безпосередній зв'язок теорії диференціальних рівнянь із додатками. Вивчаючи будь-які фізичні явища, дослідник, перш за все, створює його математичну ідеалізацію або математичну модель, записує основні закони, що керують цим явищем, у математичній формі. Найчастіше ці закони можна висловити як диференціальних рівнянь. Такими виявляються моделі різних явищ механіки суцільного середовища, хімічних реакцій, електричних і магнітних явищ та ін. дізнатися його минуле та майбутнє.
Для складання математичної моделі у вигляді диференціальних рівнянь потрібно, як правило, знати лише локальні зв'язки та не потрібна інформація про все фізичне явище в цілому. Математична модель дає можливість вивчати явище загалом, передбачити його розвиток, робити якісні оцінки вимірів, які у ньому з часом. За підсумками аналізу диференціальних рівнянь було відкрито електромагнітні хвилі.
Можна сміливо сказати, необхідність вирішувати диференціальні рівняння потреб механіки, тобто шукати траєкторії рухів, своєю чергою, стала поштовхом до створення Ньютоном нового обчислення. Через прості диференціальні рівняння йшли додатки нового числення до завдань геометрії та механіки.
Враховуючи сучасний розвиток комп'ютерної техніки та інтенсивний розвиток нового напряму – комп'ютерної математики – набули широкого поширення та попит комплекси програм, які називаються системами комп'ютерної математики.
Комп'ютерна математика - новий напрямок у науці та освіті, що виник на стику фундаментальної математики, інформаційних та комп'ютерних технологій. Система комп'ютерної математики (СКМ) - це комплекс програм, який забезпечує автоматизовану, технологічно єдину та замкнуту обробку завдань математичної спрямованості при заданні умови спеціально передбаченою мовою.
Сучасні системи комп'ютерної математики є програми з багатовіконним графічним інтерфейсом, розвиненою системою допомоги, що полегшує їх освоєння та використання. Основними тенденціями розвитку СКМ є зростання математичних можливостей, особливо у сфері аналітичних та символьних обчислень, суттєве розширення засобів візуалізації всіх етапів обчислень, широке застосування 2D- та 3D-графіки, інтеграція різних систем одна з одною та іншими програмними засобами, широкий доступ до Internet, організація спільної роботи над освітніми та науковими проектами в Internet, використання засобів анімації та обробки зображень, засобів мультимедіа та ін.
Істотною обставиною, яка донедавна перешкоджала широкому використанню СКМ в освіті, є дорожнеча професійного наукового математичного забезпечення. Однак останнім часом багато фірм, які розробляють і розповсюджують такі програми, представляють (через Internet - http://www.softline.ru) для вільного використання попередні версії своїх програм, широко використовують систему знижок для навчальних закладів, безкоштовно розповсюджують демонстраційні або пробні версії програм.
Крім того, з'являються безкоштовні аналоги систем комп'ютерної математики, наприклад Maxima, Scilab, Octave та ін.
У цьому навчальному посібнику розглядаються можливості системи комп'ютерної математики Maxima знаходження рішень диференціальних рівнянь.
Чому саме Maxima?
По-перше, система Maxima – це некомерційний проект із відкритим кодом. Maxima належить до класу програмних продуктів, які розповсюджуються на основі ліцензії GNU GPL (General Public License).По-друге, Maxima - програма на вирішення математичних завдань як у чисельному, і у символьному вигляді. Спектр її можливостей дуже широкий: дії з перетворення виразів, робота з частинами виразів, розв'язання задач лінійної алгебри, математичного аналізу, комбінаторики, теорії чисел, тензорного аналізу, статистичних завдань, побудова графіків функцій на площині та у просторі у різних системах координат тощо. буд.
По-третє, нині система Maxima має потужний, ефективний і «дружній» кросплатформовий графічний інтерфейс, який називається WxMaxima (http://wxmaxima.sourceforge.net).
Авторами книги вже протягом десяти років вивчаються системи комп'ютерної математики, такі як Mathematica, Maple, MathCad. Тому, знаючи можливості цих програмних продуктів, зокрема знаходження рішень диференціальних рівнянь, хотілося вивчити питання, пов'язані з організацією обчислень у символьному вигляді системах комп'ютерної математики, распространяемых вільно.
Цей посібник розповідає про можливості організації процесу пошуку рішень диференціальних рівнянь на базі системи Maxima, містить у собі загальні відомості щодо організації роботи в системі.
Посібник складається з 3 розділів. Перший розділ знайомить читачів з графічним інтерфейсом wxMaxima системи Maxima, особливостями роботи у ній, синтаксисом мови системи. Починається розгляд системи з того, де можна знайти дистрибутив системи та як його встановити. У другому розділі розглядаються загальні питання теорії диференціальних рівнянь, чисельні методи вирішення.
Третій розділ присвячений вбудованим функціям системи комп'ютерної математики Maxima для знаходження рішень звичайних диференціальних рівнянь 1 і 2 порядку в символьному вигляді. Також у третьому розділі показано реалізацію у системі Maxima чисельних методів розв'язання диференціальних рівнянь. Наприкінці посібника наведено завдання самостійного рішення.
Ми сподіваємося, що посібником зацікавиться широке коло користувачів і він стане їх помічником у освоєнні нового інструменту для вирішення математичних завдань.
Т.М. Губіна, Є.В. Андропова
Єлець, липень 2009
P.S. Швидкий старт: для виконання команді функцій mwMaxima потрібно безпосередньо спочатку ввести саму команду і потім натиснути crtl+Enter.
Операції математичного аналізу
Суми
Для знаходження сум призначено функцію sum. Синтаксис функції:
Sum (вираз, змінна, нижня межа зміни змінної, верхня межа зміни змінної)
Наприклад:
Якщо привласнити останньому аргументу значення системної змінної позитивної нескінченності "inf", це стане ознакою відсутності верхньої межі і буде розраховуватися нескінченна сума. Також нескінченна сума буде розраховуватися, якщо привласнити аргументу "нижня межа зміни змінної" значення системної змінної негативної нескінченності "minf". Ці значення використовується і в інших функціях математичного аналізу.
Наприклад:

Твори
Для знаходження кінцевих та нескінченних творів використовується функція product. Вона має такі ж аргументи, що і функції sum.
Наприклад:

Межі
Для знаходження меж використовується функція limit.
Синтаксис функції:
limit (вираз, змінна, точка розриву)
Якщо аргумент "точка розриву" привласнити значення "inf", то це буде ознакою відсутності кордону.
Наприклад:

Для обчислення односторонніх меж використовується додатковий аргумент, який має значення plus для обчислення меж праворуч та minus – зліва.
Наприклад, виконаємо дослідження безперервності функції arctg(1/(x - 4)). Ця функція невизначена в точці x = 4. Обчислимо межі праворуч і ліворуч:

Як бачимо, точка x = 4 є точкою розриву першого роду для цієї функції, оскільки існують межі зліва та праворуч, які дорівнюють відповідно -PI/2 і PI/2.
Диференціали
Для визначення диференціалів використовується функція diff. Синтаксис функції:
diff (вираз, змінна1, порядок похідної для змінної1 [, змінна2, порядок похідної для змінної2, ...])
де вираз – це функція, що диференціюється, другий аргумент є змінною, за якою потрібно брати похідну, третій (необов'язковий) – порядок похідної (за умовчанням – перший порядок).
Наприклад:

Взагалі обов'язковим функції diff є лише перший аргумент. У такому разі функція повертає диференціал виразу. Диференціал відповідної змінної позначається через del(ім'я змінної):

Як бачимо з синтаксису функції, користувач має можливість визначити одночасно кілька змінних диференціювання та встановити порядок для кожної з них:

Якщо використовувати параметричну функцію, форма запису функції змінюється: після імені функції записуються символи ":=", а звернення до функції здійснюється через її ім'я з параметром:

Похідна може бути обчислена у заданій точці. Це здійснюється так:

Функція diff використовується також і для позначення похідних у диференціальних рівняннях, про що йдеться нижче.
Інтеграли
Для знаходження інтегралів у системі використовується функція integrate. Для знаходження невизначеного інтеграла функції використовуються два аргументи: ім'я функції і змінна, через яку відбувається інтегрування. Наприклад:

У разі неоднозначної відповіді Maxima може поставити додаткове запитання:
Відповідь має містити текст із запитання. У разі, якщо значення змінної y більше " 0 " , це буде " positive " (позитивне), інакше - " negative " негативне). У цьому допускається введення лише першої букви слова.
Для знаходження певного інтеграла у функції слід зазначити додаткові аргументи: межі інтеграла:
Maxima допускає завдання та нескінченних меж інтегрування. Для цього для третього та четвертого аргументів функції використовуються значення "-inf" та "inf":

Для знаходження наближеного значення інтеграла в чисельному вигляді, як зазначалося раніше, слід виділити результат у комірці виведення, викликати на ній контекстне меню і вибрати з нього пункт "To Float" (перетворити на число з плаваючою точкою).

Чи здатна система обчислювати і кратні інтеграли. Для цього функції integrate вкладаються одна в одну. Нижче наводяться приклади обчислення подвійного невизначеного інтеграла та подвійного певного інтеграла:

Розв'язання диференціальних рівнянь
За своїми можливостями щодо вирішення диференціальних рівнянь Maxima відчутно поступається, наприклад, Maple. Але Maxima все ж таки дозволяє вирішувати звичайні диференціальні рівняння першого і другого порядків, а також їх системи. Для цього – залежно від мети – використовують дві функції. Для загального рішення звичайних диференціальних рівнянь використовується функція ode2, а знаходження рішень рівнянь чи систем рівнянь за початковими умовами - функція desolve.
Функція ode2 має такий синтаксис:
ode2(рівняння, залежна змінна, незалежна змінна);
Для позначення похідних диференціальних рівняннях використовується функція diff. Але в цьому випадку для відображення залежності функції від її аргументу вона записується у вигляді "diff(f(x), x), а сама функція - f(x).
приклад. Знайти загальне рішення нормального диференціального рівняння першого порядку y" - ax = 0".

Якщо значення правої частини рівняння дорівнює нулю, її взагалі можна опускати. Звичайно, права частина рівняння може містити вираз.
Як бачимо, під час розв'язання диференціальних рівнянь Maxima використовує постійну інтеграцію %c, яка з точки зору математики є довільною константою, яка визначається з додаткових умов.
Здійснити рішення звичайного диференціального рівняння можна й іншим, більш простим для користувача способом. Для цього слід виконати команду Рішення > Solve ODE (Вирішити звичайне диференціальне рівняння) і у вікні "Вирішити ОДУ" ввести аргументи функції ode2.

Maxima дозволяє вирішувати диференціальні рівняння другого порядку. Для цього також використовують функцію ode2. Для позначення похідних у диференціальних рівняннях використовується функція diff, у якій додають ще один аргумент - порядок рівняння: "diff(f(x), x, 2). Наприклад, рішення звичайного диференціального рівняння другого порядку ay" + b y = 0 матиме вигляд:

Спільно з функцією ode2 можна використовувати три функції, застосування яких дозволяє знайти рішення за певних обмежень на підставі загального рішення диференціальних рівнянь, отриманого функцією ode2:
- ic1(результат роботи функції ode2, початкове значення незалежної змінної у вигляді x = x 0 значення функції в точці x 0 у вигляді y = y 0). Призначена на вирішення диференціального рівняння першого порядку з початковими умовами.
- ic2(результат роботи функції ode2, початкове значення незалежної змінної у вигляді x = x 0 значення функції в точці x 0 у вигляді y = y 0 початкове значення для першої похідної залежної змінної щодо незалежної змінної у вигляді (y,x) = dy 0). Призначена для вирішення диференціального рівняння другого порядку з початковими умовами
- bc2(результат роботи функції ode2, початкове значення незалежної змінної у вигляді x = x 0 значення функції в точці x 0 у вигляді y = y 0 кінцеве значення незалежної змінної у вигляді x = x n значення функції в точці x n у вигляді y = yn). Призначена для вирішення крайової задачі для диференціального рівняння другого порядку.
Докладно із синтаксисом цих функцій можна ознайомитись у документації до системи.
Виконаємо розв'язання задачі Коші для рівняння першого порядку y" - ax = 0 з початковою умовою y(п) = 1.

Наведемо приклад вирішення крайової задачі для диференціального рівняння другого порядку y"+y=x з початковими умовами y(o) = 0; y(4)=1.

Слід пам'ятати, що досить часто система неспроможна вирішити диференціальні рівняння. Наприклад, при спробі знайти загальне рішення звичайного диференціального рівняння першого порядку отримуємо:

У таких випадках Maxima або видає повідомлення про помилку (як у даному прикладі) або просто повертає значення false.
Інший варіант вирішення звичайних диференціальних рівнянь першого та другого порядків призначений для пошуку рішень із початковими умовами. Він реалізується за допомогою функції desolve.
Синтаксис функції:
desolve (диференціальне рівняння, змінна);
Якщо здійснюється рішення системи диференціальних рівнянь чи є кілька змінних, то рівняння та/або змінні подаються у вигляді списку:
desolve([список рівнянь], [змінна1, змінна2,...]);
Як і попереднього варіанта, для позначення похідних в диференціальних рівняннях використовується функція diff, що має вигляд "diff(f(x), x).
Початкові значення для змінної надаються функцією atvalue. Ця функція має такий синтаксис:
atvalue(функція, змінна = точка, значення у точці);
В даному випадку передбачається, що значення функцій та (або) їх похідних задаються для нуля, тому синтаксис функції atvalue має вигляд:
atvalue(функція, змінна = 0, значення у точці "0");
приклад. Знайти рішення диференціального рівняння першого порядку y" = sin (x) з початковою умовою.

Зауважимо, що і за відсутності початкової умови функція також спрацює та видасть результат:

Це дозволяє перевірити рішення для конкретного початкового значення. Справді, підставляючи отриманий результат значення y(0) = 4, якраз і отримуємо y(x) = 5 - cos(x).
Функція desolve дозволяє вирішувати системи диференціальних рівнянь з початковими умовами.
Наведемо приклад розв'язання системи диференціальних рівнянь  із початковими умовами y(0) = 0; z(0) = 1.
із початковими умовами y(0) = 0; z(0) = 1.

Обробка даних
Статистичний аналіз
Система дозволяє розрахувати основні статистичні описові статистики, з допомогою яких описуються найбільш загальні властивості емпіричних даних. До основних описових статистик відносять середню, дисперсію, стандартне відхилення, медіану, моду, максимальне та мінімальне значення, розмах варіації та квартилі. Можливості Maxima у цьому плані дещо скромні, але більшість цих статистик за її допомогою розрахувати досить просто.
Найпростішим способом розрахунку статистичних описових статистик є використання палітри Statistics (Статистика).

Панель містить низку інструментів, згрупованих у чотири групи.
- Статистичні показники (описові статистики):
- mean (середня арифметична);
- median (медіана);
- variance (дисперсія);
- deviation (середнє квадратичне відхилення).
- Тести.
- Побудова п'яти типів графіків:
- гістограма (Histogram). Використовується насамперед у статистиці зображення інтервальних рядів розподілу. Під час її побудови по осі ординат відкладають частини чи частоти, але в осі абсцис - значення ознаки;
- діаграма розсіювання (діаграма кореляції, поле кореляції, Scatter Plot) – графік за точками, коли точки не з'єднуються. Використовується для відображення даних для двох змінних, одна з яких є факторною, а інша результативною. З її допомогою здійснюється графічне представлення пар даних у вигляді множини точок ("хмари") на координатній площині;
- стрічкова діаграма (Bar Chart) – графік у вигляді вертикальних стовпців;
- секторна або кругова діаграма (Pie Chart). Така діаграма поділена на кілька сегментів-секторів, площа кожного з яких пропорційна їхній частині;
- коробкова діаграма (коробка з вусами, скринька з вусами, Box Plot, box-and-whisker diagram). Саме вона найчастіше використовується для зображення статистичних даних. Інформація такого графіка є дуже змістовною та корисною. Він одночасно відображає кілька величин, які характеризують варіаційний ряд: мінімальне та максимальне значення, середню та медіану, перший та третій квартиль.
- Інструменти для зчитування чи створення матриці. Для використання інструментів палітри необхідно мати початкові дані як матриці - одномірного масиву. Його можна створити в документі з поточною сесією і надалі підставляти його назву як вхідні дані у вікнах інструментів палітри аналогічно рішенню рівнянь за допомогою панелі загальних математичних дій (General Math). Можна і безпосередньо задавати дані у вікнах введення вхідних даних. У цьому випадку вони вводяться у прийнятому в системі вигляді, тобто у квадратних дужках і через кому. Зрозуміло, перший варіант є значно кращим, оскільки він вимагає лише одноразового введення даних.
Окрім панелі, всі статистичні інструменти можуть бути використані також за допомогою відповідних функцій.
Maxima- комп'ютерна система, що дозволяє працювати із символьними, чисельними виразами. Підтримує операції розкладання ряд, диференціювання, перетворення Лапласа, інтегрування. Програмі нестрашні прості диференціальні рівняння, матриці та тензори, системи лінійних рівнянь, списки, вектори, багаточлени, множини. Система комп'ютерних обчислень може проводити розрахунки з високим рівнем точності. Використовує цілі числа, дрібні вирази. Додаток вміє будувати графіки у двовимірному чи тривимірному вимірі. Має посібник, де докладно викладено, як працювати з утилітою, які оператори підтримуються системою математичних операцій. Програма чудово підходить любителям комп'ютерної алгебри: студентам, викладачам, аспірантам.


- Працює з математичними числовими та символьними виразами.
- Підтримує роботу зі списками, багаточленами, матрицями, тензорами, диференціальними рівняннями та системами лінійних рівнянь.
- Підтримує операції розкладання у ряд, диференціювання, перетворення Лапласа, інтегрування.
- Здійснює розрахунки з високим ступенем точності.
- використовує цілі числа, дробові вирази.
- Вміє будувати графіки у двомірному чи тривимірному вимірі.
- Підходить любителям комп'ютерної алгебри.
- має доступну документацію для ознайомлення з роботою системи.
- Не впливає на продуктивність та швидкість роботи операційного середовища.
– Є підтримка російської мови.
Недоліки програми
- Відсутня портативна версія.- Процесор із тактовою частотою 1200 MHz або більш потужний.
- Оперативна пам'ять 256 Мб або більше.
- Вільне місце на твердому диску від 185 Мб.
- Архітектура з розрядністю 32 біти або 64 біти (x86 або x64).
- Операційна система Windows XP, Windows Vista, Windows 7, Windows 8
Багатофункціональні калькулятори: Таблиці порівняння
| Назва програми | Російською | Дистрибутиви | Інсталятор | Популярність | Розмір | Індекс |
| ★ ★ ★ ★ ★ | 48.7 Мб | 100 | ||||
| ★ ★ ★ ★ ★ | 59.8 Мб | 99 | ||||
| ★ ★ ★ ★ ★ | 1.3 Мб | 86 | ||||
У системі Maxima є багато вбудованих функцій. Для кожної вбудованої функції можна отримати опис документації, що міститься в довідковій системі. Викликати довідку можна за допомогою функціональної клавіші F1. Також у Maxima є спеціальна функція, яка видає інформацію з документації за конкретними словами. Скорочена версія виклику цієї функції: ?? name (Рис.12). Тут? - це ім'я оператора, і аргумент потрібно відокремлювати від нього пропуском. Оператор? видає список тих розділів допомоги та імен функцій, які містять заданий текст, після чого пропонують ввести номер того розділу або опис тієї функції, які потрібно подивитися:
Рис.12. Виклик довідки по команді системи Maxima.
Зауважимо, що у системі Maxima немає чіткого розмежування між операторами та функціями. Більш того, кожен оператор – це насправді функція.
Усі функції та оператори Maxima працюють не тільки з дійсними, але й комплексними числами. Самі комплексні числа записуються в формі алгебри, з уявною одиницею, позначеної через %i; тобто у вигляді a+b*%i, де аі b- відповідно дійсна та уявна частини числа.
Розглянемо синтаксис базових функційсистеми Maxima.
1. Арифметичні оператори: +, -, *, /, ->. Приклад:

3. Логічні оператори: and, or, not. Приклад:

4. Функція знаходження факторіалу числа: !
Факторіал заданий у найбільш загальному вигляді і є, по суті, гамма-функцію (точніше, x! = gamma(x+1)), тобто визначений на багатьох комплексних чисел, крім негативних цілих. Факторіал від натурального числа (і нуля) автоматично спрощується до натурального числа.
![]()
5. Функція знаходження напівфакторіалу чила: !! (твір всіх парних (для парного операнда) чи непарних чисел, менших чи рівних цьому).
6. Функція заперечення синтаксичного рівності: #Запис a#b еквівалентна not a=b. 
7. Функція знаходження модуля числа x: abs(x) Модуль визначено всім комплексних чисел. Приклад:

8. Функція, що повертає знак числа x: signum(x)

9. Функції, що повертають найбільше та найменше значення із заданих дійсних чисел: max(x1,...,xn) та min(x1,...,xn).

10. Деякі вбудовані математичні функції:
| sqrt (x) | Квадратний корінь з x |
| acos (x) | Арккосинус аргументу х |
| acosh (x) | Гіперболічний арккосинус аргументу х |
| acot (x) | Арккотангенс аргументу х |
| acoth (x) | Гіперболічний арккотангенс аргументу х |
| acsc (x) | Арккосеканс аргументу х |
| acsch (x) | Гіперболічний арккосеканс аргументу х |
| asec (x) | Арксеканс аргументу х |
| asech (x) | Гіперболічний арксеканс аргументу х |
| asin(x) | Арксинус аргументу х |
| asinh (x) | Гіперболічний арксинус аргументу х |
| atan (x) | Арктангенс аргументу х |
| atanh (x) | Гіперболічний арктангенс аргументу х |
| cosh (x) | Гіперболічний косинус аргументу х |
| coth (x) | Гіперболічний котангенс аргументу х |
| csc (x) | Косеканс аргументу х |
| csch (x) | Гіперболічний косеканс аргументу х |
| sec(x) | Секанс аргументу х |
| sech (x) | Гіперболічний секанс аргументу х |
| sin(x) | Синус аргументу х |
| sinh(x) | Гіперболічний синус аргументу х |
| tan(x) | Тангенс аргументу х |
| tanh (x) | Гіперболічний тангенс аргументу х |
| log(x) | Натуральний логарифм х |
| exp(x) | Експонента х |
11. Функції до роботи з матрицями:
determinant – знаходження визначника матриці:
eigenvalues – знаходження власних значень матриці:
invert- Отримання зворотної матриці:

minor- Визначає мінор матриці. Перший аргумент – матриця, другий та
третій – індекси рядка та стовпця відповідно:
rank– ранг матриці:
submatrix- Повертає матрицю, отриману з вихідним видаленням
відповідних рядків та (або) стовпців. Як параметри слідують
номери рядків, вихідна матриця, номери стовпців, що видаляються.

transpose- транспонування матриці:

У мові системи Maxima закладені основні оператори, які є в будь-якій мові програмування. Розглянемо їх.
Оператори надання значень (іменування виразів).
1. Оператор ":" (оператор завдання значення змінної).
2. Оператор «:=» (оператор завдання функції користувача).
3.Розширені варіанти операторів присвоєння та завдання функції, що позначаються відповідно через:: і::=.
Використання оператора завдання функції користувача значно полегшує роботу з нею, оскільки до неї можна звертатися по імені та легко та зручно обчислювати значення функції у заданих точках.
Приклад: знайдемо значення функції f (x,y)=cosx + sin yу точці

Оператор циклу.Оператор циклу може задаватися кількома способами. Спосіб завдання залежить від того, чи відомо наперед скільки разів необхідно виконати тіло циклу.
Приклад: завдання циклу для виведення значень змінної ав діапазоні від -3 до 10 з кроком 5:

Наступною важливою можливістю системи Maxima є робота зі списками та масивами.
Для формування списків використовується команда makelist. Наприклад, за допомогою команди

ми сформували список з ім'ям x, що складається із десяти елементів, значення яких знаходяться за формулою .
Для формування масивів використовується команда array. Наприклад, за допомогою команди,
![]()
ми сформували двовимірний масив A, що складається з 10 рядків та 5 стовпців. Для заповнення масиву елементами скористаємося циклом із параметром. Наприклад,
Для виведення елементів масиву на екран можна скористатися командою:
Масив можна формувати без попереднього оголошення. У наступному прикладі ми сформували одновимірний масив x, що складається з 5 елементів, значення яких обчислюються формулою x( i)=sin i

Незручність роботи з масивами полягає в тому, що виведення значень елементів масиву здійснюється у стовпець. Набагато зручніше, якщо значення масиву (двовимірного) виводяться у вигляді матриці. Для цього можна скористатися командою genmatrix. Наприклад, для формування двовимірного масиву (матриці) слід задати команду у наступному вигляді:
Виведемо отриманий масив:

6. Найпростіші перетворення виразів.
За умовчанням у системі Maxima є активною функція автоспрощення, тобто. система намагається спростити вираз, що вводиться сама без будь-якої команди.
приклад. Нехай потрібно знайти значення наступного числового виразу:
Задамо вираз за правилами мови системи Maxima.

Як бачимо, система у відповідь вивела значення виразу, хоча ми не задали жодної команди.
Як же змусити систему вивести не результат, а вираз? Для цього функцію спрощення треба відключити за допомогою simp: false$. Тоді отримаємо:

Щоб активувати функцію спрощення, треба задати команду simp:true$. Функція автоспрощення може працювати як із числовими, так і з деякими не числовими виразами. Наприклад,

При введенні ми можемо звертатися до будь-якого з попередніх осередків на її ім'я, підставляючи його в будь-які вирази. Крім того, останній осередок виведення позначається через %, а останній осередок введення - через _. Це дозволяє звертатися до останнього результату, не відволікаючись, який його номер. Але такими зверненнями до осередків зловживати зайве, оскільки за переоцінювання всього документа чи його окремих осередків введення може статися суперечність між номерами осередків.
приклад. Знайти значення виразу та збільшити отриманий результат у 5 разів.

Бажано замість імен осередків використовувати змінні та присвоювати їх імена будь-яким виразам. І тут у вигляді значення змінної може бути будь-яке математичне вираз.
Значення імен змінних зберігаються протягом всієї роботи з документом. Нагадаємо, що якщо необхідно зняти визначення зі змінною, то це можна зробити за допомогою функції kill(name), де name - ім'я виразу, що знищується; причому це може бути як ім'я, призначене вами, так і будь-яка комірка введення або виведення. Так само можна очистити всю пам'ять і звільнити всі імена, ввівши команду kill(all) (або вибрати меню Махта->Очистить пам'ять(Clear Memory)). У цьому випадку очистяться навіть всі осередки вводу-виводу, і їх нумерація знову почнеться з одиниці.
Функція автоспрощення далеко не завжди здатна спростити вираз. На додаток до неї є цілий ряд команд, які призначені для роботи з виразами: раціональними та ірраціональними. Розглянемо деякі з них.
rat (вираз) - перетворює раціональний вираз до канонічної форми: розкриває всі дужки, потім приводить все до спільного знаменника, підсумовує та скорочує; наводить всі числа в кінцевому десятковому записі до раціональних. Канонічна форма автоматично «скасовується» у разі будь-яких перетворень, які не є раціональними.
ratsimp (вираз) - спрощує вираз за рахунок раціональних перетворень. Працює навіть «вглиб», тобто ірраціональні частини висловлювання не розглядаються як атомарні, а спрощуються, зокрема, і всі раціональні елементи всередині них
fullratsimp(вираз) - функція спрощення раціонального вираження методом послідовного застосування до переданого виразу функції ratsimp(). За рахунок цього функція працює дещо повільніше, ніж ratsimp(), проте дає більш надійний результат.
expand (вираз) - розкриває дужки у виразі всіх рівнях вкладеності. На відміну від функції ratexpand(), не приводить дроби-складові до спільного знаменника.
radcan (вираз) - функція спрощення логарифмічних, експоненційних функцій та статечних з нецілими раціональними показниками, тобто коренів (радикалів).
Часто при спробі спрощення вираження у Maxima може відбуватися насправді лише його ускладнення. Збільшення результату може відбуватися через те, що невідомо, які значення можуть набувати змінні, що входять до виразу. Щоб уникнути цього, слід накладати обмеження на значення, які може приймати змінна. Робиться це за допомогою функції assume (умова). Тому в деяких випадках найкращого результату можна досягти, комбінуючи radcan() з ratsimp() або fullratsimp().