Елементи комбінаторики. Секрети везіння чи покроковий алгоритм виграшу у лотереї Варіанти комбінацій із 5 цифр
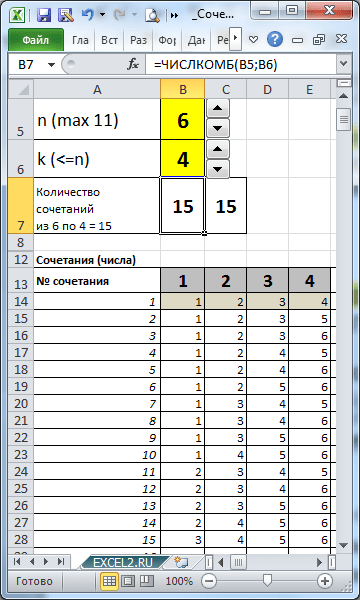
Підрахуємо в MS EXCEL кількість поєднань із n елементів по k. За допомогою формул виведемо на аркуш всі варіанти поєднань (англійський переклад терміна: Combinations without repetition).
Поєднаннями з n різних елементів до k елементів називаються комбінації, які відрізняються хоча б одним елементом. Наприклад, нижче перераховані ВСІ 3-х елементні поєднання, взяті з множини, що складається з 5 елементів (1; 2; 3; 4; 5):
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примітка: Це стаття про підрахунок кількості поєднань з використанням MS EXCEL Теоретичні основи радимо прочитати у спеціалізованому підручнику. Вивчати поєднання за цією статтею – погана ідея.
Відмінність Поєднань від Розміщень
Виведення всіх комбінацій Поєднань
У прикладному файлі створені формули для виведення всіх Сполучень для заданих n і k.
Задаючи за допомогою кількість елементів множини (n) і кількість елементів, яку ми вибираємо з нього (k), за допомогою формул можна вивести всі Поєднання.
Завдання
Автовоз може перевозити по 4 легкові машини. Необхідно перевезти 7 різних машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Скільки різними способами можна заповнити перший автовоз? Конкретне місце машини в автовозі не має значення.
Нам потрібно визначити число Поєднань 7 машин на 4-х місцях автовозу. Тобто. n=7, а k=4. Виявляється, що таких варіантів = ЧИСЛКОМБ (7; 4) дорівнює 35.
Довільним чином порівняємо маркам машин числові значення та зробимо скорочення назв марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
Все N елементів, і жоден не повторюється, це завдання про кількість перестановок. Рішення можна знайти простим. На першому місці в ряді може стояти будь-який з елементів N, отже, виходить N варіантів. На другому місці – будь-який, крім того, який уже був використаний для першого місця. Отже, кожному з N вже знайдених варіантів є (N - 1) варіантів другого місця, і кількість комбінацій стає N*(N - 1).
Це можна повторити інших елементів ряду. Для самого останнього місця залишається тільки один варіант - останній елемент, що залишився. Для передостаннього – два варіанти, і так далі.
Отже, для низки з N неповторних елементів можливих перестановок дорівнює добутку всіх від 1 до N. Цей твір називається факторіалом числа N і позначається N! (Читається «ен факторіал»).
У попередньому випадку кількість можливих елементів і кількість місць ряду збігалися, і їх число дорівнювало N. Але можлива ситуація, коли в ряду менше місць, ніж можливих елементів. Іншими словами, кількість елементів у вибірці дорівнює деякому числу M, причому M< N. В этом случае задача определения количества возможных комбинаций может иметь два различных варианта.
По-перше, може знадобитися порахувати загальну кількість можливих способів, якими можна побудувати ряд M елементів з N. Такі способи називаються розміщеннями.
По-друге, дослідника може цікавити кількість способів, якими можна вибрати M елементів з N. При цьому порядок розташування елементів вже не важливий, але будь-які два варіанти повинні відрізнятися між собою хоча б одним елементом. Такі методи називаються поєднаннями.
Щоб знайти кількість розміщень M елементів з N, можна вдатися до такого ж способу міркувань, як і у випадку з перестановками. На першому місці тут, як і раніше, може стояти N елементів, на другому (N - 1), і так далі. Але для останнього місця кількість можливих варіантів дорівнює не одиниці, а (N - M + 1), оскільки коли розміщення буде закінчено, залишиться ще (N - M) невикористаних елементів.
Таким чином, число розміщень M елементів з N дорівнює добутку всіх цілих чисел від (N - M + 1) до N, або, що те ж саме, приватному N!/(N - M)!.
Очевидно, що кількість поєднань M елементів з N буде менше кількості розміщень. Для кожного можливого поєднання є M! можливих розміщень, які від порядку елементів цього поєднання. Отже, щоб знайти цю кількість, потрібно розділити число розміщень M елементів з N на N!. Іншими словами, кількість поєднань по M елементів N дорівнює N!/(M!*(N - M)!).
Багато любителів лотерей задаються цілком справедливим питанням, як виграти в лотерею 5 з 36. Перш ніж ми спробуємо відповісти на ці питання, необхідно ознайомитися з правилами і порахувати ймовірність виграшу в лотерею 5 з 36.
Лотерею Гослото 5 із 36 можна назвати розумним вибором із усіх існуючих лотерей на даний момент, оскільки ця лотерея має максимальні шанси на виграш головного призу.
Звичайно, говорячи про максимальні шанси, ми повинні розуміти, що це лотерея і шанси на основний виграш джекпоту не є великими.
Кількість комбінацій у лотереї 5 з 36
Логічно буде перейти до фактів та озвучити точні цифри. Кількість комбінацій лотереї 5 з 36:
376992
триста сімдесят шість дев'ятсот дев'яносто два
і лише одна з них стає виграшною.
Ми вище писали, що гравці в 5 з 36 роблять розумно – тому, що в порівнянні з лотерею Гослото 6 з 45, тут шанси виграти суперприз майже в 22 рази більше!
Думаєте як виграти у Гослото великий приз – грайте у 5 із 36! Так, ця лотерея не накопичує великого джекпота, однак і шанси на виграш має значно більші.
Вірогідності в лотереї 5 з 36
Всі ймовірності збігів кількості чисел, що випали, наводяться в таблиці нижче:
| Збігів | Ймовірність |
| 0 | |
| 1 | 1:3 |
| 2 | 1:9 |
| 3 | 1:82 |
| 4 | 1:2433 |
| 5 | 1:376992 |
Як розрахувати виграшну комбінацію 5 з 36
Розгорнута система – у гонитві за 100% виграшем джекпоту
100% шанс на виграш у лотерею дасть лише розгорнута система, до якої входитимуть усі 36 чисел, тобто ставка на всі можливі комбінації. Однак таку ставку буде зробити неможливо і не розумно з кількох причин:
1. Обмеження за правилами. Кількість вибраних чисел у розгорнутій ставці згідно з правилами лотереї не перевищує 11, оформити таку ставку в якій в одному квитку буде закреслено всі числа не можна.
2. Припустимо, що хтось вручну або автоматично все ж таки зважиться скупити всі можливі комбінації на майбутній тираж.
При вартості квитка в 80 рублів на це знадобиться дуже істотна сума в 30 159 360 рублів.
Така ставка була б цілком реалізована, якби була логічно її економічна складова. Джекпот Гослото 5 з 36 ніколи навіть близько не підбирався до цієї суми, і ніколи не підбереться до цієї суми навіть близько. Виграш джекпоту за такої ставки звичайно буде з ймовірністю 100%, але сума виграшу по ньому не покриє необхідну суму витратити на покупку такої кількості квитків.
Чотири розгорнуті системи – у гонитві за виграшем.
Всі 36 чисел лотереї можна розкласти порівну чотири мішечки.

У кожному мішечку буде по 9 чисел. Загалом у ході розіграшу випадає п'ять чисел.
Відповідно, якщо перші чотири чисел, що випали, опиняться в різних мішечках, то п'яте число опиниться в одному з мішечків, в якому вже є число, що випало. Тобто як не крути при найгіршому варіанті один з мішечків міститиме 2 виграшних числа, тобто виявиться виграшним.
Таким чином, щоб гарантовано виграти в лотерею, потрібно зробити чотири розгорнуті системи, в яких будуть задіяні всі цифри.
Вартість чотирьох таких ставок при сумі квитка в 80 рублів дорівнюватиме 40 320 рублів при гарантованому виграші 80 рублів.
Здавалося б, економічна доцільність такої ставки також сумнівна, але не слід забувати, що така ставка може зірвати і приз більшої категорії, але тут уже без жодних 100% гарантій.
Так, ймовірність збігу трьох чисел у такій ставці буде менше 30%, а ймовірність виграшу джекпоту дорівнюватиме стандартній ймовірності, як при купівлі 504 квитків з випадковими комбінаціями.
Ще кілька систем гри в Гослото 5 із 36
Наша програма під назвою Нострадамус намагається вгадати виграшну комбінацію найближчого тиражу на основі статистичного аналізу та інших факторів, формуючи лише одну комбінацію.
Неповні системи 5 з 36 є щадним за фінансами аналогом розгорнутих систем. Багато гравців знаходять цю систему основною для своєї гри.
Збалансована стратегія піддає елементарному математичному аналізу комбінації, що випали.
Висновок
Лотерея залишається лотереєю – азартним захопленням, яке приносить нечисленним переможцям мільйонні виграші. У статті розглянуто деякі можливі методики виграшу та теорія ймовірності у лотереї Гослото 5 із 36.
Читайте також інші записи у блозі:
Система виграшу в лотерею від багаторазового переможця
Комбінаторика - це розділ математики, у якому вивчаються питання, скільки різних комбінацій, підпорядкованих тим чи іншим умовам, можна скласти із заданих об'єктів. Основи комбінаторики дуже важливі з метою оцінки ймовірностей випадкових подій, т.к. саме вони дозволяють підрахувати принципово можливу кількість різних варіантів розвитку подій.
Основна формула комбінаторики
Нехай є k груп елементів, причому i група складається з n i елементів.
Виберемо по одному елементу з кожної групи. Тоді загальна кількість N способів, якими можна зробити такий вибір, визначається співвідношенням N = n 1 * n 2 * n 3 * ... * n k .Пояснимо це правило простому прикладі. Нехай є дві групи елементів, причому перша група складається з n 1 елементів, а друга - n 2 елементів. Скільки різних пар елементів можна скласти із цих двох груп, таким чином, щоб у парі було по одному елементу від кожної групи? Допустимо, ми взяли перший елемент із першої групи і, не змінюючи його, перебрали всі можливі пари, змінюючи лише елементи з другої групи. Таких пар цього елемента можна скласти n 2 . Потім ми беремо другий елемент із першої групи і також складаємо для нього всі можливі пари. Таких пар також буде n 2 .
Так як у першій групі всього n 1 елемент, всього можливих варіантів буде n 1 * n 2 .приклад 2.
Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?Рішення:
n 1 =6 (т.к. як перша цифра можна взяти будь-яку цифру з 1, 2, 3, 4, 5, 6), n 2 =7 (т.к. як другу цифру можна взяти будь-яку цифру з 0 , 1, 2, 3, 4, 5, 6), n 3 =4 (т.к. як третя цифра можна взяти будь-яку цифру з 0, 2, 4, 6).
Отже, N = n 1 * n 2 * n 3 = 6 * 7 * 4 = 168. У разі, коли всі групи складаються з однакового числа елементів, тобто. n 1 =n 2 =...n k =n вважатимуться, кожен вибір виробляється з однієї й тієї групи, причому елемент після вибору знову повертається у групу. Тоді число всіх способів вибору дорівнює n k. Такий спосіб вибору комбінаторики носить назву
вибірки із поверненням.приклад 3.
Скільки всіх чотирицифрових чисел можна становити з цифр 1, 5, 6, 7, 8?Рішення.
До кожного розряду чотиризначного числа є п'ять можливостей, отже N=5*5*5*5=5 4 =625. Розглянемо безліч, які з n елементів. Це безліч у комбінаториці називається.
генеральною сукупністю
Число розміщень з n елементів mВизначення 1. Розміщенням з n елементів по m у комбінаториці називається будь-якийупорядкований набір елементів поз Розміщенням зрізних елементів, вибраних з генеральної сукупності в
елементів.приклад 4.
Різними розміщеннями з трьох елементів (1, 2, 3) по два будуть набори (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2) ). Розміщення можуть відрізнятися друг від друга як елементами, і їх порядком.
Число розміщень у комбінаториці позначається A n m і обчислюється за такою формулою:Примітка:
n!=1*2*3*...*n (читається: "ен факторіал"), крім того вважають, що 0!=1.Приклад 5
Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?т.к. непарних цифр п'ять, саме 1, 3, 5, 7, 9, це завдання зводиться до вибору і розміщення дві різні позиції двох із п'яти різних цифр, тобто. вказаних чисел буде:
Визначення 2. Поєднаннямз Розміщенням з n елементів поу комбінаториці називається будь-який невпорядкований набірупорядкований набір елементів порізних елементів, вибраних з генеральної сукупності в Розміщенням зелементів.
Приклад 6. Для множини (1, 2, 3) поєднаннями є (1, 2), (1, 3), (2, 3).
Число поєднань з n елементів m
Число поєднань позначається C n m і обчислюється за такою формулою:
![]()
Приклад 7.Скільки способами читач може вибрати дві книжки із шести наявних?
Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?Число методів дорівнює числу поєднань із шести книжок по дві, тобто. одно:
![]()
Перестановки з n елементів
Визначення 3. Перестановкоюз Розміщенням зелементів називається будь-який у комбінаториці називається будь-якийцих елементів.
Приклад 7a.Різними перестановками множини, що складається з трьох елементів (1, 2, 3) є: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), ( 3, 2, 1), (3, 1, 2).
Число різних перестановок з елементів n позначається P n і обчислюється за формулою P n = n!.
Приклад 8.Скільки способами сім книг різних авторів можна розставити на полиці в один ряд?
Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?це завдання про кількість перестановок семи різних книг. Є P 7 =7!=1*2*3*4*5*6*7=5040 способів здійснити розміщення книг.
Обговорення. p align="justify"> Ми бачимо, що число можливих комбінацій можна порахувати за різними правилами (перестановки, поєднання, розміщення) причому результат вийде різний, т.к. Принцип підрахунку і самі формули відрізняються. Уважно подивившись визначення, можна побачити, що результат залежить від кількох чинників одночасно.
По-перше, з того, з якої кількості елементів ми можемо комбінувати їх набори (наскільки велика генеральна сукупність елементів).
По-друге, результат залежить від того, який розмір набори елементів нам потрібні.
І останнє, важливо знати, чи є для нас суттєвим порядок елементів у наборі. Пояснимо останній чинник на такому прикладі.
Приклад 9.На батьківських зборах присутні 20 осіб. Скільки існує різних варіантів складу батьківського комітету, якщо до нього мають увійти 5 осіб?
Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?У цьому прикладі нас не цікавить порядок прізвищ у списку Комітету. Якщо в результаті в його складі будуть одні й ті ж люди, то за змістом для нас це один і той самий варіант. Тому ми можемо скористатися формулою для підрахунку числа поєднаньіз 20 елементів по 5.
Інакше будуть справи, якщо кожен член комітету спочатку відповідає за певний напрямок роботи. Тоді при тому самому списковому складі комітету, всередині нього можливо 5! варіантів перестановокякі мають значення. Кількість різних (і за складом, і за сферою відповідальності) варіантів визначається у цьому випадку числом розміщеньіз 20 елементів по 5.
Завдання для самоперевірки
1. Скільки трицифрових парних чисел можна становити з цифр 0, 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися?
2. Скільки існує п'ятизначних чисел, які однаково читаються зліва направо та праворуч наліво?
3. У класі десять предметів та п'ять уроків на день. Скільки способами можна скласти розклад на один день?
4. Скільки можна вибрати 4 делегати на конференцію, якщо в групі 20 осіб?
5. Скільки способами можна розкласти вісім різних листів по восьми різних конвертах, якщо кожен конверт кладеться лише одне лист?
6. З трьох математиків та десяти економістів треба скласти комісію, що складається з двох математиків та шести економістів. Скільки способами це можна зробити?