Алгоритм шифрування RSA. Приклад алгоритму шифрування RSA Технологія реалізації алгоритму RSA

Вступ 3

Основна частина 5

1Історія створення 5

2Опис алгоритму 5

2.1 Створення ключів 6

2.2Шифрування та розшифрування 6

2.3Приклад використання 7

Висновок 9

Список використаних джерел 10

Вступ

Криптографія – спеціальна система зміни звичайного листа, використовувана з метою зробити текст зрозумілим лише обмеженої кількості осіб, знають цю систему .

Криптографія - наука про захист інформації з використанням математичних методів.

Сучасна криптографія включає:

симетричні криптосистеми;

асиметричні криптосистеми;

системи електронного цифрового підпису (ЕЦП);

хеш-функції;

керування ключами;

отримання прихованої інформації;

квантова криптографія.

Симетричне шифрування - симетричними називаються алгоритми, в яких для шифрування та дешифрування використовується той самий (відомий тільки відправнику та одержувачу) секретний ключ.

Поширені алгоритми симетричного шифрування:

AES (англ. Advanced Encryption Standard) – американський стандарт шифрування;

ГОСТ 28147-89 – вітчизняний стандарт шифрування даних;

DES (англ. Data Encryption Standard) – стандарт шифрування даних у США до AES;

3DES (Triple-DES, потрійний DES);

IDEA (англ. International Data Encryption Algorithm);

SEED – корейський стандарт шифрування даних;

Camellia – сертифікований для використання в Японії шифр;

XTEA - найбільш простий у реалізації алгоритм.

Асиметричні криптоалгоритми покликані насамперед усунути основний недолік симетричних криптосистем – складність управління та розповсюдження ключів.

Основою всіх асиметричних криптоалгоритмів є велика обчислювальна складність відновлення відкритого тексту без знання закритого ключа.

Приклади асиметричних криптоалгрітмів:

Diffie-Hellmann;

RSA - Rivest, Shamir, Adelman - заснований на складності завдання розкладання на множники великих чисел за короткий час;

DSA – Digital Signature algorithm, стандарт США;

ГОСТ Р 34.10 - 94, 2001, стандарти РФ.

У цьому рефераті докладно розглянемо асиметричний криптоалгоритм шифрування – алгоритм RSA.

Основна частина

Алгоритм RSA (літерна абревіатура від прізвищ Rivest, Shamir та Adleman) – криптографічний алгоритм з відкритим ключем, що ґрунтується на обчислювальній складності завдання факторизації великих цілих чисел. Криптосистема RSA стала першою системою, придатною і для шифрування, і цифрового підпису.

Історія створення

Опублікована в листопаді 1976 року стаття Вітфілда Діффі та Мартіна Хеллмана «Нові напрямки в криптографії» перевернула уявлення про криптографічні системи, заклавши основи криптографії з відкритим ключем. Розроблений згодом алгоритм Діффі – Хеллмана дозволяв двом сторонам отримати спільний секретний ключ, використовуючи незахищений канал зв'язку. Однак цей алгоритм не вирішував проблему автентифікації. Без додаткових коштів користувачі не могли бути впевнені, з ким вони згенерували спільний секретний ключ.

Вивчивши цю статтю, троє вчених Рональд Рівест (Ronald Linn Rivest), Аді Шамір (Adi Shamir) і Леонард Адлеман (Leonard Adleman) з Массачусетського Технологічного Інституту (MIT) приступили до пошуків математичної функції, яка б дозволяла реалізувати сформульовану Уітфілдом Діффі та Мартіном Хеллманом модель криптографічної системи з відкритим ключем. Після роботи над більш ніж 40 можливими варіантами їм вдалося знайти алгоритм, заснований на відмінності в тому, наскільки легко знаходити великі прості числа і наскільки складно розкладати на множники добуток двох великих простих чисел, який згодом отримав назву RSA. Система була названа за першими буквами прізвищ її творців.

Опис алгоритму

Першим етапом будь-якого асиметричного алгоритму є створення пари ключів – відкритого та закритого та поширення відкритого ключа "по всьому світу".

Створення ключів

Для алгоритму RSA етап створення ключів складається з наступних операцій:

Число називається відкритою експонентою

Шифрування та розшифрування

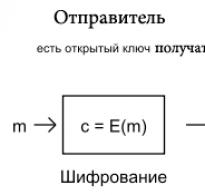
Припустимо, відправник хоче надіслати одержувачу повідомлення .

Повідомлення є цілі числа в інтервалі від 0 до , тобто. . На малюнку 1 представлено схему алгоритму RSA.

Рисунок 1 – Схема алгоритму RSA

Алгоритм Відправника:

Алгоритм Одержувача:

Рівняння (1) та (2), на яких заснована схема RSA, визначають взаємно зворотні перетворення множини.

Приклад використання

У таблиці 1 наведено приклад використання алгоритму RSA. Відправник відправив зашифроване повідомлення "111111" і одержувач, використовуючи свій закритий ключ, розшифрував його.

Таблиця 1 - Поетапне виконання алгоритму RSA

Висновок

У цьому рефераті детально розглянуто алгоритм асиметричного шифрування RSA. Була описана історія його створення, описані алгоритми створення ключів, шифрування та розшифрування. Також наведено приклад практичного використання алгоритму RSA.

Список використаних джерел

Семенов Ю.А. Протоколи Internet / / М.: Проспект, 2011. - 114 с.

Бєляєв А.В. Методи та засоби захисту інформації // ЧФ СПбДТУ, 2010. - 142с.

Венбо М. Сучасна криптографія. Теорія та практика // М.: Вільямс, 2005. – 768 с.

Шнайєр Б. Прикладна криптографія. Протоколи, алгоритми, вихідні тексти // М.: Тріумф, 2002. – 816 с.

Алгоритм RSA // Інтернет ресурс: http://ua.wikipedia.org/wiki/Rsa

У другій частині ми розглянемо популярний алгоритм RSA, де для шифрування використовується публічний ключ. Але спочатку хочу попередити вас ще раз. Код, поданий у цій статті, призначений лише для ознайомлювальних цілей. Криптографія - дуже широка і складна область, і щоб у вас не було проблем, я не рекомендую шифрувати інформацію за допомогою мого виробу.

У другій частині ми розглянемо популярний алгоритм RSA, де для шифрування використовується публічний ключ. Але спочатку хочу попередити вас ще раз. Код, поданий у цій статті, призначений лише для ознайомлювальних цілей. Криптографія - дуже широка і складна область, і щоб у вас не було проблем, я не рекомендую шифрувати інформацію за допомогою мого виробу.

Алгоритм RSA

Шифрування з використанням публічного ключа

Шифрування з допомогою публічного ключа використовується повсюдно. Якщо ви хоч раз оплачували щось в інтернеті, то вже користувалися цим методом (я сподіваюся!). Відразу виникає питання про те, як працює цей захист. Якщо я вводжу номер своєї кредитної картки, щоб щось купити, чому, крім адресата, ніхто не може підглянути ці відомості? Наведу метафору. Щоб відкрити сейф, вам потрібен ключ (або молоток, але, на щастя, сейфи та замки захищені від такого роду діячів). У шифруванні з використанням публічного ключа відбувається приблизно те саме. Ви показуєте замок на загальний огляд, але ключ від цього замку є тільки у обраних, а іншими способами відчинити двері фактично нереально.

RSA – один із алгоритмів, що реалізують вищезазначену схему. Крім того, ми можемо використовувати цей алгоритм, щоб підтвердити справжність нашої особистості. Якщо ви, використовуючи секретний ключ, надсилаєте комусь зашифроване повідомлення, адресат за допомогою публічного ключа може розшифрувати ваше послання. Ця технологія дозволяє підписувати повідомлення, і цим підтверджується справжність відправника.

Демо-програма на базі алгоритму RSA

Залежно від структури використовуваних ключів методи шифрування поділяються на:

• симетричне: стороннім особам може бути відомий алгоритм шифрування, але невідома невелика порція секретної інформації - ключа, однакового для відправника та одержувача повідомлення; Приклади: DES, 3DES, AES, Blowfish, Twofish, ГОСТ 28147-89
• асиметричне шифрування: стороннім особам може бути відомий алгоритм шифрування, і, можливо, відкритий ключ, але невідомий закритий ключ, відомий тільки одержувачу. Криптографічні системи з відкритим ключем в даний час широко застосовуються в різних мережевих протоколах, зокрема, в протоколах TLS і його попереднику SSL (що лежать в основі HTTPS), а також SSH, PGP, S/MIME і т.д. використовує асиметричне шифрування - .

На даний момент асиметричне шифрування на основі відкритого ключа RSA (розшифровується, як Rivest, Shamir and Aldeman – творці алгоритму) використовує більшість продуктів на ринку інформаційної безпеки.

Його криптостойкость грунтується на складності розкладання на множники великих чисел, саме - виняткової труднощі завдання визначити секретний ключ виходячи з відкритого, оскільки цього потрібно вирішити завдання існування дільників цілого числа. Найбільш криптостійкі системи використовують 1024-бітові та великі числа.

Розглянемо алгоритм RSA з практичного погляду.

Для початку необхідно згенерувати відкритий та секретні ключі:

• Візьмемо два великі прості числа p and q.
• Визначимо n, як наслідок множення p on q (n= p*q).
• Виберемо випадкове число, яке назвемо d. Це число має бути взаємно простим (не мати жодного спільного дільника, крім 1) із результатом множення (p-1)*(q-1).
• Визначимо таке число е, якого є істинним наступне співвідношення (e*d) mod ((p-1)*(q-1))=1.
• Назвемо відкритим ключем числа e і n, а секретним - d і n.

Для того, щоб зашифрувати дані з відкритого ключа (e,n), необхідно наступне:

• розбити текст, що шифрується, на блоки, кожен з яких може бути представлений у вигляді числа M(i)=0,1,2..., n-1(тобто тільки до n-1).
• зашифрувати текст, що розглядається як послідовність чисел M(i) за формулою C(i)=(M(I)^e)mod n.

Щоб розшифрувати ці дані, використовуючи секретний ключ (d,n), потрібно виконати такі обчислення: M(i) = (C(i)^d) mod n. В результаті буде отримано безліч чисел M(i), які є вихідним текстом.

Наступний приклад наочно демонструє алгоритм шифрування RSA:

Зашифруємо та розшифруємо повідомлення "САВ" за алгоритмом RSA. Для простоти візьмемо невеликі числа – це скоротить наші розрахунки.

• Виберемо p = 3 і q = 11.
• Визначимо n = 3 * 11 = 33.
• Hайдем (p-1) * (q-1) = 20. Отже, d дорівнюватиме, наприклад, 3: (d=3).
• Виберемо число е за такою формулою: (e * 3) mod 20 = 1. Значить е дорівнюватиме, наприклад, 7: (e=7).
• Представимо повідомлення, що шифрується, як послідовність чисел в діапазоні від 0 до 32 (не забувайте, що закінчується на n-1). Літера А = 1, В = 2, С = 3.

Тепер зашифруємо повідомлення, використовуючи відкритий ключ (7,33)

C1 = (3 ^ 7) mod 33 = 2187 mod 33 = 9;
C2 = (1 ^ 7) mod 33 = 1 mod 33 = 1;
C3 = (2 ^ 7) mod 33 = 128 mod 33 = 29;

Тепер розшифруємо дані, використовуючи закритий ключ (3,33).

M1 = (9 ^ 3) mod 33 = 729 mod 33 = 3 (С);
M2 = (1 ^ 3) mod 33 = 1 mod 33 = 1 (А);
M3 = (29 ^ 3) mod 33 = 24389 mod 33 = 2 (В);

Дані розшифровані!

Нарешті настав час зайнятися описом RSA-криптосистеми. Крім пояснення, як вона працює, ми повинні детально обговорити її безпеку; інакше кажучи, чому так важко зламати повідомлення, зашифроване RSA-криптосистемою?

§ 12.1. Про початок і кінець

Щоб реалізувати систему шифрування RSA, призначену для одного користувача, необхідно вибрати два різних простих числа р і q і обчислити їх добуток Прості р і q зберігаються в таємниці, тоді як число стає частиною відкритого ключа. У § 12.5 ми докладно обговоримо метод вибору простих складових ключа, а також те, як цей вибір пов'язаний із надійністю системи.

Повідомлення (яке можна вважати цілим числом) шифрується шляхом зведення в деякий ступінь за модулем Тому спочатку ми повинні знайти спосіб представити текст повідомлення у вигляді списку класів за модулем Це, насправді, ще не процес шифрування, а лише підготовка повідомлення до того, щоб його можна було зашифрувати.

Для простоти припустимо, що текст повідомлення містить лише слова, записані великими літерами. Отже, повідомлення, зрештою, - послідовність літер і прогалин. Перший крок полягає у заміні кожної літери повідомлення числом, яке вибирається з наступної таблиці:

(Див. скан)

Пробіл між словами замінюється на число 99. Зробивши цю процедуру, ми отримаємо число, можливо, дуже велике, якщо повідомлення було довгим. Однак, це ще не остаточне число, якого ми прагнемо, а всього лише набір класів по модулю І тепер нам потрібно розбити чисельне уявлення повідомлення на шматочки, кожен з яких - натуральне число, що не перевершує Ці шматочки прийнято називати блоками повідомлення.

Наприклад, чисельна вистава девізу «ПІЗНАЙ СЕБЕ» виглядає так:

Вибравши прості ми отримаємо твір Тому чисельне уявлення повідомлення, виписане вище, потрібно розбити на блоки, менші ніж 23 393. Наведемо одне з таких розбиття.

Звісно, ​​вибір блоків не однозначний, але й зовсім довільний. Наприклад, щоб уникнути двозначностей на стадії

розшифровки не слід виділяти блоки, що починаються з нуля.

При розшифруванні повідомлення, зашифрованого системою шифрування RSA, одержують послідовність блоків. Потім їх з'єднують разом та отримують чисельне подання повідомлення. І лише після заміни чисел буквами відповідно до наведеної таблиці можна буде прочитати вихідне повідомлення.

Зверніть увагу, що кожна буква таблиці кодується двозначним числом. Так робиться для запобігання плутанині. Припустимо, ми пронумерували букви по порядку, починаючи з першого, тобто. А відповідає 1, Б - 2, і таке інше. У цьому випадку ми не зможемо точно сказати, чи позначає блок 12 пару літер або лише одну літеру дванадцяту літеру алфавіту. Звичайно, для чисельного представлення повідомлення можна використовувати будь-яку однозначну відповідність між літерами і числами, наприклад, кодування, при якому переклад повідомлення в цифрову форму автоматично виконується комп'ютером.

§ 12.2. Шифрування та дешифрування

Повідомлення, підготовлене до шифрування за методом § 12.1, складається з послідовності блоків, кожен з яких - число, менше, ніж тепер обговоримо, як шифрується кожен блок. Для цього нам знадобиться число, що дорівнює добутку простих і натуральне число, оборотне за модулем тобто. число, що задовольняє умові

Нагадаємо, що за відомими р і q число легко обчислюється. Справді,

Пара називається відкритим, або кодуючим ключем криптосистеми RSA, яку ми описуємо. Нехай блок повідомлення, тобто ціле число, що задовольняє нерівності Символом, будемо позначати блок зашифрованого повідомлення, відповідний Він обчислюється за таким правилом:

Зауважимо, кожен блок повідомлення шифрується окремо. Тому зашифроване повідомлення фактично складається з окремих закодованих блоків. Більше того, ми не можемо об'єднати ці блоки в одне велике число, оскільки розшифрувати повідомлення стане неможливо. Незабаром ми побачимо причину цього.

Повернемося до прикладу, який почали розглядати у першому параграфі. Ми зафіксували так що Тепер потрібно вибрати число Нагадаємо, що воно має бути взаємно простим з Найменше просте число, що не ділить 23088, дорівнює 5. Покладемо Щоб закодувати перший блок повідомлення з § 12.1, ми повинні визначити відрахування числа 25245 по модулю 23 393. С За допомогою програми символьних обчислень (або калькулятора, якщо вистачить терпіння) ми отримаємо, що шукане відрахування дорівнює 22 752. Отже, все ж таки зашифроване повідомлення представляється наступною послідовністю блоків:

Подивимося, як декодуються блоки зашифрованого повідомлення. Щоб приступити до дешифрування, нам необхідно знати і зворотний елемент до модуля Останній з них - це натуральне число, яке ми позначатимемо через Пара називається секретним, або декодуючим ключем системи шифрування RSA. Якщо а - блок зашифрованого повідомлення, то відповідне його дешифрування

Виходить у результаті операції:

Перш ніж повернутись до прикладу, необхідно дати деякі коментарі. По-перше, обчислити дуже легко, якщо знати, дійсно, секретний ключ визначається за допомогою розширеного алгоритму Евкліда. По-друге, якщо блок вихідного повідомлення, ми маємо право очікувати рівності Іншими словами, декодуючи блок шифрованого повідомлення, ми сподіваємося дізнатися відповідний блок вихідного. Те, що це так і буде, не випливає безпосередньо з описаного вище алгоритму, але ми докладно обговоримо в наступному параграфі.

Нарешті, як ми стверджували у вступі і протягом усієї книги, для злому RSA-криптосистеми необхідно розкласти на множники, тому що для дешифрування повідомлення потрібно знати. Однак після того, як робота системи докладно описана, ясно, що останнє твердження не зовсім точно. Щоб прочитати шифрування, крім самого потрібно знати лише зворотний елемент по модулю Тому для злому системи достатньо обчислити при відомих Виявляється, це обчислення рівносильне розкладанню числа на множники, як ми переконаємося в § 12.4.

В обговорюваному прикладі Для визначення застосуємо розширений алгоритм Евкліда до числа і 5.

(Див. скан)

Таким чином, Отже, зворотним до 5 по модулю буде -9235 і

Найменше натуральне число, порівнянне з -9235 по модулю Значить, для розкодування блоку шифрованого повідомлення ми повинні звести його в ступінь 13853 по модулю 23393. У нашому прикладі перший закодований блок - це 22752. Обчислюючи відрахування числа 28 32 , отримаємо Зауважте, що навіть за таких малих числах вимоги, що висуваються під час роботи RSA-криптосистеми, перевищують можливості більшості кишенькових калькуляторів.

§ 12.3. Чому вона працює?

Як ми вже зазначали раніше, описані вище кроки призводять до працюючої криптосистеми, тільки якщо в результаті декодування кожного блоку шифрованого повідомлення буде відновлюватися відповідний блок вихідного. Припустимо, що ми маємо справу з системою RSA, що має відкритий ключ і секретний ключ Дотримуючись позначень § 12.2, нам потрібно показати, що для будь-якого цілого числа, що задовольняє нерівність, виконується тотожність

Насправді, достатньо довести, що

Дійсно, як 6, так і невід'ємні цілі числа, менші Тому вони можна порівняти за модулем тоді і тільки тоді, коли вони рівні. Це, зокрема, пояснює, чому ми розбиваємо чисельне подання повідомлення на блоки, менші. Крім того, звідси видно, що блоки

закодованого повідомлення необхідно записувати окремо: інакше наші міркування не працюватимуть.

З рецептів шифрування та дешифрування випливає, що

Оскільки елементи взаємно зворотні за модулем знайдеться таке натуральне до, що Більше того, за умовою, числа більше Отже, Підставляючи замість твору в рівняння (3.1), отримуємо

Тепер скористаємося теоремою Ейлера, яка стверджує, що Звідси.

і ми б повністю отримали доказ, якби в нього не закралася маленька помилочка.

Уважно переглянувши наші міркування, Ви помітите, що ми не враховували умов теореми Ейлера. Насправді, як застосовувати теорему, необхідно переконатися у взаємної простоті чисел За цим, начебто, слід стежити під час підготовки повідомлення до шифрування, тобто. під час розбиття чисельного подання повідомлення на блоки потрібно добиватися впевненості в тому, що всі блоки, що виходять, взаємно прості з На щастя, в цьому немає необхідності, тому що насправді порівняння виконано для будь-якого блоку. І помилка криється не в результаті, який ми хочемо довести, а лише в самому доказі. Правильний підхід полягає в міркуваннях, використаних за підтвердження теореми Корселта у розділі 7.

Де різні прості числа. Визначимо відрахування числа за модулями

обчислення для обох простих чисел аналогічні, ми пропрацюємо в деталях тільки випадок. Отже, ми вже переконалися в тому, що

для деякого цілого Отже,

Ми хотіли б тепер застосувати теорему Ферма, але маємо право зробити це тільки якщо не ділить Нехай ця вимога виконана. Тоді і ми отримуємо, що

Замінивши теорему Ферма теоремою Ейлера, ми не вирішили проблеми, що виникла: порівняння справедливе тільки для деяких, але не для всіх блоків. Однак тепер блоки, для яких міркування не проходять, повинні ділитися на Далі, якщо ділить як 6, так і порівняні з 0 по модулю а значить порівнянні між собою. Таким чином, порівняння, що доводиться, справедливе і в цьому випадку. Отже, порівняння є істинним для будь-якого цілого числа Зверніть увагу на те, що ми не. могли використовувати подібне міркування, коли застосовували теорему Ейлера до Дійсно, нерівність не означає порівняння, тому що число складене.

Отже, ми довели, що Аналогічно доводиться порівняння Іншими словами, ділиться і на і на Але прості прості числа, так що Таким чином, лема з § 3.6 гарантує нам, що ділить А так як ми маємо для будь-якого цілого числа Іншими словами, Як ми зазначили на початку параграфа, цього достатньо для доказу рівності, оскільки обидві його частини - невід'ємні цілі числа, менші підсумовуючи, можна стверджувати, що

алгоритм попереднього параграфа призводить до практичної криптосистеми. Тепер потрібно переконатись у її надійності.

§ 12.4. Чому система надійна?

Нагадаємо, що RSA - система шифрування з відкритим ключем, що складається з добутку різних простих чисел і натурального числа оборотного за модулем Подивимося уважно, що можна зробити для злому RSA, якщо все, що відомо, це пара

Щоб розкодувати блок, зашифрований за допомогою RSA, ми повинні дізнатися число зворотне до модуля Проблема в тому, що практично єдиний відомий спосіб зробити це ґрунтується на застосуванні розширеного алгоритму Евкліда до Однак для обчислення за формулою з § 9.4 нам потрібно знати що підтверджує початкове твердження : злом RSA вимагає розкладання на множники А оскільки проблеми розкладання мають важливий характер, система RSA безпечна.

Можна, звичайно, припустити, що коли-небудь хто-небудь відкриє алгоритм, що обчислює без інформації про множників числа.

відомі, то ми з легкістю обчислюємо Дійсно,

так що сума простих дільників, що шукаються, відома. Далі,

тому різниця теж відома. Тепер, вирішуючи просту систему лінійних рівнянь, легко находимо розкладання на множники.

Значить, алгоритм, що обчислює фактично, розкладає число на множники, так що це одного поля ягідки. Але заспокоюватися поки що рано. Можна піти далі у своїх фантазіях і припустити, що хтось винайшов алгоритм, що визначає безпосередньо по Але Так що, якщо нам відомі то ми знаємо число, кратне Виявляється, такої інформації теж достатньо для розкладання Імовірнісний алгоритм, що призводить до такого розкладання, можна знайти в. У вправі 7 наведено схожий (але більш простий) алгоритм розкладання у припущенні, що криптосистему Рабіна можна зламати. Він дасть вам уявлення про ймовірнісний алгоритм .

Залишається остання можливість для злому: спроба відновлення блоку безпосередньо з відрахування по модулю Якщо досить велике, то систематичний перебір всіх можливих кандидатів для пошуку єдиний вихід. Ніхто ще не придумав нічого кращого. Ми перерахували основні аргументи, які пояснюють, чому злом RSA-криптосистеми вважається рівносильним розкладанню на прості множники, хоча суворого доказу цього твердження поки що немає.

§ 12.5. Вибір простих

З попереднього обговорення випливає, що для безпеки RSA-криптосистеми важливо правильно вибрати прості числа Природно якщо вони малі, то система легко зламується. Однак недостатньо вибрати великі дійсно, навіть якщо р і q величезні, але різниця мала, їх твір легко розкладається на множники за допомогою алгоритму Ферма (див. § 3.4).

Це не пуста розмова. У 1995 році два студенти одного американського університету зламали версію RSA, що перебуває у громадському користуванні. Таке стало можливим через поганий вибір простих множників системи.

З іншого боку, RSA використовувалася протягом тривалого часу і, якщо прості співмножники вибрані ретельно, система насправді виявляється досить надійною. Таким чином, будь-якому програмісту системи шифрування RSA необхідний ефективний метод успішного вибору простих чисел.

Припустимо, ми хочемо створити RSA-криптосистему з відкритим ключем, в якому ціле число має близько знаків. Спочатку виберемо просте число знаків якого лежить між візьмемо близьким до В даний час рекомендований персонального використання розмір ключа дорівнює 768 бітам, тобто. має приблизно складатися із 231 цифри. Щоб побудувати таке число, нам знадобиться два простих, скажімо, зі 104 та 127 знаків. Зверніть увагу, що вибрані в такий спосіб прості досить далекі друг від друга, тобто. застосування алгоритму Ферма для розкладання цієї ситуації непрактично. Крім того, нам потрібно переконатися в тому, що в розкладанні чисел на прості множники беруть участь не лише малі дільники, а й великі. Справді, інакше, число стає легкою здобиччю деяких відомих алгоритмів розкладання (див. ). Розглянемо тепер метод, з допомогою якого знаходять прості числа, які задовольняють переліченим умовам.

Спочатку нам знадобиться один простий результат про розподіл простих чисел. Нагадаємо, що позначає кількість простих, що не перевершують х. Враховуючи теорему про прості числа, ми бачимо, що для великих х число приблизно дорівнює де натуральний логарифм

на підставі (див. § 4.5). Нехай дуже велике, якесь позитивне число. Ми хочемо оцінити кількість простих чисел, що лежать між прикинути різницю Завдяки теоремі про прості числа і властивості логарифму, різниця приблизно дорівнює

Припускаючи, що дуже мало, ми можемо вважати значення рівним 0 і отримати розумну оцінку різниці. Отже, кількість простих, укладених між приблизно рівною. 10]).

Припустимо, що нам потрібно вибрати просте число на околиці цілого х. Для визначеності вважатимемо, що х має порядок , а просте шукаємо в інтервалі від х до Було б корисно знати заздалегідь, скільки простих чисел знаходиться в цьому інтервалі. Для оцінки кількості простих можна скористатися щойно отриманим результатом. У прикладі величина має дуже маленький порядок: Тому за формулою, виписаної вище, ми укладаємо, що у інтервалі між лежить приблизно

прості числа. Наприкінці другого параграфа глави 11 ми сформулювали стратегію, призначену для доказу простоти цього непарного числа. Вона складається з трьох кроків.

Схема Райвеста - Шаміра - Адлемана (RSA) в даний час є єдиною, що отримала широке визнання і схемою шифрування, що практично застосовується, з відкритим ключем.

Схема RSA є блочним шифром, в якому і відкритий текст, і шифрований текст представляються цілими числами з діапазону від 0 до п- 1 для деякого п.

Відкритий текст шифрується блоками, кожен із яких містить двійкове значення, менше деякого заданого числа п.Це означає, що довжина блоку повинна бути не більшою за log2(«). На практиці довжина блоку вибирається рівною 2 добітам, де 2 до Схема, розроблена Райвестом, Шаміром та Адлеманом, заснована на виразах зі ступенями. Шифрування та дешифрування для блоку відкритого тексту М та блоку шифрованого тексту С можна подати у вигляді наступних формул:

Як відправник, і одержувач повинні знати значення п.Відправник знає значення е,і лише одержувачу відоме значення d.Таким чином, ця схема є алгоритмом шифрування з відкритим ключем KU= (е, п),та особистим ключем KR = (d, п).

Щоб цей алгоритм міг бути використаний для шифрування з відкритим ключем, повинні бути виконані такі вимоги:

Повинні існувати такі значення е, dі п,що M ed = M(mod д)всім М п.

Повинні відносно легко обчислюватись IVT та З с1всім значень М п.

Мабуть практично неможливо визначити dза наявними їй п.

Проаналізуємо спочатку першу вимогу, інші розглянемо пізніше. Необхідно знайти співвідношення виду

Тут якнайкраще підійде слідство з теореми Ейлера: для таких будь-яких двох простих чисел рі qі таких будь-яких двох цілих чисел піт,що n=pqn0 та довільного цілого числа довиконуються такі співвідношення:

де ф(я) є функцією Ейлера, значення якої дорівнює числу позитивних цілих чисел, менших пі взаємно простих з п.

У разі простих рі qмаємо ф (pq) - (р - 1 )(q - 1). Тому необхідне співвідношення виходить за умови

Це еквівалентно наступним співвідношенням:

тобто. їй dє взаємно зворотними за модулем ф(я). Зверніть увагу, що відповідно до правил арифметики у класах відрахувань це може мати місце лише тоді, коли d(а отже і е)є взаємно простим з ф(і). В еквівалентному записі (ф(/7), d)=.

Тепер ми маємо все, щоб представити схему RSA. Компонентами схеми є:

рі q- два простих числа (секретні, вибираються);

п - pq(Відкрите, обчислюється);

таке е, що (ф(я), е)= 1,1 е

d = е л(mod ф(/?)) (секретне, обчислюється).

Особистий ключ складається з (d, n),а відкритий з (Е, п).Припустимо, що користувач А опублікував свій відкритий ключ, і тепер користувач збирається переслати йому повідомлення М.

Тоді користувач обчислює шифроване повідомлення

Отримавши цей шифрований текст, користувач А дешифрує його, обчислюючи

Має сенс навести тут обґрунтування цього алгоритму. Були обрані їй dтакі, що

Значить, лишає вигляд кц>(п)+.Але за теорією Ейлера, для таких будь-яких двох простих чисел рі quцілих чисел п = pqnМ, що виконуються співвідношення

Тому

Тепер маємо

Таблиця 10.1 резюмує алгоритм RSA, але в рис. 10.1 показаний приклад застосування. У цьому прикладі ключі обчислюються таким чином:

• 1. Вибираються два простих числа: р- 7 wq- 17.
• 2. Обчислюється п = pq= 7 x 17 = 119.
• 3. Обчислюється ф (п) - (р-) (q - 1) = 96.
• 4. Вибирається е, взаємно просте з ф (п)= 96 і менше, ніж ф(я); у разі = 5.
• 5. Визначається таке d,що de= 1 (mod 96) та d 96. Відповідним значенням буде d= 77, оскільки 77 x 5 = 385 = 4 x 96 + 1.
• 6. В результаті виходять відкритий ключ KU = (5, 119) та особистий ключ KR = (77, 119).

У цьому прикладі показано використання цих ключів з відкритим текстом, що вводиться, М = 19. При шифруванні 19 зводиться в п'яту ступінь, що в результаті дає 2 476 099. В результаті поділу на 119 визначається залишок, рівний 66. Отже, 19 5 = 66(mod 119) і тому шифрованим текстом буде 66. Після дешифрування з'ясовується, що

Мал. 10.1.

Таблиця 10.1