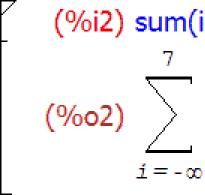Maximálny popis. Ako pracovať s maximom
Matematický balík Maxima je jednou z najlepších bezplatných náhrad za MathCAD.
Túto učebnicu (vo formáte pdf) je možné použiť v rámci disciplín matematická analýza, diferenciálne rovnice, aplikačné softvérové balíky atď. v rôznych špecializáciách na inštitúciách vyššieho odborného vzdelávania, ak štátny vzdelávací štandard stanovuje štúdium časti „Diferenciál rovnice“, ako aj v rámci voliteľných predmetov. Môže byť užitočný aj pri oboznamovaní sa s počítačovými matematickými systémami v špecializovaných triedach všeobecnovzdelávacích inštitúcií s hĺbkovým štúdiom matematiky a informatiky.
- Predslov
- Kapitola 1. Základy práce v počítačovom matematickom systéme Maxima
- 1.1. O systéme Maxima
- 1.2. Inštalácia Maxima na osobný počítač
- 1.3. Rozhranie hlavného okna Maxima
- 1.4. Práca s bunkami v Maxime
- 1.5. Práca so systémom pomoci Maxima
- 1.6. Funkcie a príkazy systému Maxima
- 1.7. Riadenie procesu výpočtu v Maxima
- 1.8. Jednoduché transformácie výrazov
- 1.9. Riešenie algebraických rovníc a ich sústav
- 1.10. Možnosti grafiky
- Kapitola 2. Numerické metódy riešenia diferenciálnych rovníc
- 2.1. Všeobecné informácie o diferenciálnych rovniciach
- 2.2. Numerické metódy riešenia Cauchyho úlohy pre obyčajnú diferenciálnu rovnicu prvého rádu
- 2.2.1. Eulerova metóda
- 2.2.2. Eulerova-Cauchyho metóda
- 2.2.3. Metóda Runge-Kutta 4 rády presnosti
- 2.3. Riešenie okrajových úloh pre obyčajné diferenciálne rovnice metódou konečných rozdielov
- 2.4. Grid metóda riešenia parciálnych diferenciálnych rovníc
- Kapitola 3. Hľadanie riešení diferenciálnych rovníc v systéme Maxima
- 3.1. Vstavané funkcie na hľadanie riešení diferenciálnych rovníc
- 3.2. Riešenie diferenciálnych rovníc a ich sústav v symbolickej forme
- 3.3. Konštrukcia trajektórií a smerových polí diferenciálnych rovníc.
- 3.4. Implementácia numerických metód na riešenie Cauchyho úlohy pre obyčajné diferenciálne rovnice
- 3.4.1. Eulerova metóda
- 3.4.2. Eulerova-Cauchyho metóda
- 3.4.3. Metóda Runge-Kutta
- 3.5. Implementácia metódy konečných rozdielov na riešenie okrajovej úlohy pre obyčajné diferenciálne rovnice
- 3.6. Implementácia mriežkovej metódy pre parciálne diferenciálne rovnice
- Úlohy na samostatné riešenie
- Literatúra
Predslov
Teória diferenciálnych rovníc je jedným z najväčších odvetví modernej matematiky. Jednou z hlavných čŕt diferenciálnych rovníc je priama súvislosť medzi teóriou diferenciálnych rovníc a aplikáciami. Pri štúdiu akéhokoľvek fyzikálneho javu si výskumník v prvom rade vytvorí jeho matematickú idealizáciu alebo matematický model, zapíše základné zákony, ktorými sa tento jav riadi, v matematickej forme. Veľmi často sa tieto zákony dajú vyjadriť vo forme diferenciálnych rovníc. Ukázalo sa, že ide o modely rôznych javov mechaniky kontinua, chemických reakcií, elektrických a magnetických javov atď. Štúdiom výsledných diferenciálnych rovníc spolu s ďalšími podmienkami, ktoré sú spravidla špecifikované vo forme počiatočných a okrajových podmienok , matematik získava informácie o vyskytujúcom sa jave, niekedy môže zistiť jeho minulosť a budúcnosť.
Na zostavenie matematického modelu vo forme diferenciálnych rovníc spravidla potrebujete poznať iba lokálne súvislosti a nepotrebujete informácie o celom fyzickom jave ako celku. Matematický model umožňuje študovať jav ako celok, predpovedať jeho vývoj a kvalitatívne hodnotiť merania, ktoré sa v ňom vyskytujú v priebehu času. Elektromagnetické vlny boli objavené na základe analýzy diferenciálnych rovníc.
Môžeme povedať, že potreba riešiť diferenciálne rovnice pre potreby mechaniky, teda nájsť trajektórie pohybu, bola zasa podnetom pre Newtona k vytvoreniu nového počtu. Aplikácie nového počtu na problémy geometrie a mechaniky sa uskutočnili pomocou obyčajných diferenciálnych rovníc.
Berúc do úvahy moderný vývoj výpočtovej techniky a intenzívny vývoj nového smeru - počítačovej matematiky - sú softvérové balíky nazývané počítačové matematické systémy rozšírené a žiadané.
Počítačová matematika je nový smer vo vede a vzdelávaní, ktorý vznikol na priesečníku základnej matematiky, informačných a počítačových technológií. Počítačový matematický systém (SCM) je súbor programov, ktoré poskytujú automatizované, technologicky jednotné a uzavreté spracovanie matematických problémov pri špecifikácii podmienok v špeciálne navrhnutom jazyku.
Moderné počítačové matematické systémy sú programy s viacokenným grafickým rozhraním a vyvinutým systémom nápovedy, ktorý uľahčuje ich učenie a používanie. Hlavnými trendmi vo vývoji SCM sú rast matematických schopností, najmä v oblasti analytických a symbolických výpočtov, výrazné rozšírenie vizualizačných nástrojov pre všetky stupne výpočtov, široké využitie 2D a 3D grafiky, integrácia rôznych systémy medzi sebou a iným softvérom, široký prístup na internet, organizovanie spolupráce na vzdelávacích a vedeckých projektoch na internete, využívanie nástrojov na animáciu a spracovanie obrazu, multimediálne nástroje a pod.
Významnou okolnosťou, ktorá donedávna bránila širokému využívaniu SCM vo vzdelávaní, sú vysoké náklady na profesionálny vedecký matematický softvér. V poslednom čase však mnohé spoločnosti vyvíjajúce a distribuujúce takéto programy prezentujú (prostredníctvom internetu - http://www.softline.ru) predchádzajúce verzie svojich programov na bezplatné použitie, vo veľkej miere využívajú systém zliav pre vzdelávacie inštitúcie a distribuujú demo resp. skúšobné verzie bezplatných programov
Okrem toho sa objavujú bezplatné analógy počítačových matematických systémov, napríklad Maxima, Scilab, Octave atď.
Tento tutoriál pojednáva o možnostiach počítačového matematického systému Maxima pri hľadaní riešení diferenciálnych rovníc.
Prečo práve Maxima?
Po prvé, systém Maxima je neziskový open source projekt. Maxima patrí do triedy softvérových produktov, ktoré sú distribuované pod GNU GPL (General Public License).Po druhé, Maxima je program na riešenie matematických problémov v numerickej aj symbolickej forme. Rozsah jeho možností je veľmi široký: akcie na transformáciu výrazov, práca s časťami výrazov, riešenie problémov lineárnej algebry, matematická analýza, kombinatorika, teória čísel, tenzorová analýza, štatistické úlohy, vytváranie grafov funkcií v rovine a v priestore. v rôznych súradnicových systémoch atď. d.
Po tretie, Maxima má teraz výkonné, efektívne a užívateľsky prívetivé multiplatformové GUI s názvom WxMaxima (http://wxmaxima.sourceforge.net).
Autori knihy sa už desať rokov venujú štúdiu počítačových matematických systémov ako Mathematica, Maple, MathCad. Preto, poznajúc možnosti týchto softvérových produktov, najmä na hľadanie riešení diferenciálnych rovníc, som chcel študovať problematiku organizácie výpočtov v symbolickej forme vo voľne distribuovaných počítačových matematických systémoch.
Táto príručka hovorí o možnostiach organizácie procesu hľadania riešení diferenciálnych rovníc na báze systému Maxima a obsahuje všeobecné informácie o organizácii práce v systéme.
Návod pozostáva z 3 kapitol. Prvá kapitola oboznamuje čitateľov s grafickým rozhraním wxMaxima systému Maxima, funkciami práce v ňom a syntaxou jazyka systému. Úvaha o systéme začína tým, kde nájdete distribúciu systému a ako ju nainštalovať. Druhá kapitola rozoberá všeobecné otázky teórie diferenciálnych rovníc a numerických metód na ich riešenie.
Tretia kapitola je venovaná vstavaným funkciám počítačového matematického systému Maxima na hľadanie riešení obyčajných diferenciálnych rovníc 1. a 2. rádu v symbolickej forme. Aj v tretej kapitole je ukázaná implementácia numerických metód riešenia diferenciálnych rovníc v systéme Maxima. Na konci návodu sú úlohy na samostatné riešenie.
Dúfame, že príručka zaujme široké spektrum používateľov a stane sa ich pomocníkom pri osvojovaní si nového nástroja na riešenie matematických úloh.
T.N. Gubina, E.V. Andropovej
Yelets, júl 2009
P.S. Rýchly štart: vykonávať príkazy a funkcií v mwMaxima, musíte najprv zadať samotný príkaz a potom stlačiť crtl+Enter.
Operácie matematickej analýzy
čiastky
Funkcia súčtu sa používa na nájdenie súčtu. Syntax funkcie:
Súčet (výraz, premenná, spodná hranica zmeny premennej, horná hranica zmeny premennej)
Napríklad:
Ak poslednému argumentu priradíte hodnotu systémovej premennej kladné nekonečno "inf", bude to znamenať absenciu hornej hranice a vypočíta sa nekonečný súčet. Nekonečný súčet sa vypočíta aj vtedy, ak priradíte hodnotu zápornej nekonečnej systémovej premennej "minf" k argumentu "dolná hranica zmeny premennej". Rovnaké hodnoty sa používajú v iných funkciách matematickej analýzy.
Napríklad:

Tvorba
Ak chcete nájsť konečné a nekonečné produkty, použite funkciu produktu. Má rovnaké argumenty ako súčtová funkcia.
Napríklad:

Limity
Ak chcete nájsť limity, použite funkciu limit.
Syntax funkcie:
limit (výraz, premenná, bod zlomu)
Ak je argument "bod prerušenia" nastavený na "inf", bude to znamenať absenciu orámovania.
Napríklad:

Pre výpočet jednostranných limitov sa používa dodatočný argument, ktorý má hodnotu plus pre výpočet limitov vpravo a mínus pre vľavo.
Preštudujme si napríklad spojitosť funkcie arctan(1/(x - 4)). Táto funkcia je v bode x = 4 nedefinovaná. Vypočítajme limity vpravo a vľavo:

Ako vidíme, bod x = 4 je bodom nespojitosti prvého druhu pre túto funkciu, pretože naľavo a napravo sú hranice, ktoré sa rovnajú -PI/2 a PI/2.
Diferenciály
Funkcia diff sa používa na nájdenie diferenciálov. Syntax funkcie:
diff(výraz, premenná1, poradie derivácie pre premennú1 [,premenná2, poradie derivácie pre premennú2,...])
kde výraz je funkcia, ktorá je diferencovaná, druhý argument je premenná, vzhľadom na ktorú musí byť derivácia braná, tretí (voliteľný) je poradie derivácie (štandardne - prvý poriadok).
Napríklad:

Vo všeobecnosti sa pre funkciu diff vyžaduje iba prvý argument. V tomto prípade funkcia vráti diferenciál výrazu. Rozdiel zodpovedajúcej premennej je označený del(názov premennej):

Ako vidíme zo syntaxe funkcie, užívateľ má možnosť súčasne definovať niekoľko diferenciačných premenných a nastaviť poradie pre každú z nich:

Ak použijete parametrickú funkciu, zmení sa forma zápisu funkcie: za názvom funkcie sa píšu symboly ":=" a k funkcii sa pristupuje cez jej názov s parametrom:

Deriváciu možno vypočítať v danom bode. Robí sa to takto:

Diff funkcia sa tiež používa na označenie derivácií v diferenciálnych rovniciach, ako je uvedené nižšie.
Integrály
Ak chcete nájsť integrály v systéme, použite funkciu integrovať. Na nájdenie neurčitého integrálu funkcie sa používajú dva argumenty: názov funkcie a premenná, nad ktorou prebieha integrácia. Napríklad:

Ak je odpoveď nejednoznačná, Maxima môže položiť ďalšiu otázku:
Odpoveď musí obsahovať text z otázky. V tomto prípade, ak je hodnota premennej y väčšia ako "0", bude "kladná" a inak - "negatívna". V tomto prípade je možné zadať iba prvé písmeno slova.
Ak chcete nájsť určitý integrál vo funkcii, musíte zadať ďalšie argumenty: limity integrálu:
Maxima tiež umožňuje nekonečné integračné limity. Na tento účel sa hodnoty „-inf“ a „inf“ používajú pre tretí a štvrtý argument funkcie:

Ak chcete nájsť približnú hodnotu integrálu v číselnej forme, ako bolo uvedené vyššie, mali by ste vybrať výsledok vo výstupnej bunke, zavolať na ňu kontextovú ponuku a vybrať z nej položku „To Float“ (previesť na číslo s pohyblivou rádovou čiarkou) .

Systém je tiež schopný vypočítať viac integrálov. Na tento účel sú integrované funkcie vnorené jedna do druhej. Nasledujú príklady výpočtu dvojitého neurčitého integrálu a dvojitého určitého integrálu:

Riešenia diferenciálnych rovníc
Z hľadiska svojich schopností pri riešení diferenciálnych rovníc je Maxima výrazne nižšia ako napríklad Maple. Maxima vám však stále umožňuje riešiť bežné diferenciálne rovnice prvého a druhého rádu, ako aj ich systémy. Na tento účel sa v závislosti od účelu používajú dve funkcie. Na všeobecné riešenie obyčajných diferenciálnych rovníc sa používa funkcia ode2 a na hľadanie riešení rovníc alebo sústav rovníc na základe počiatočných podmienok funkcia desolve.
Funkcia ode2 má nasledujúcu syntax:
ode2(rovnica, zavisle premenna, nezavisle premenna);
Diff funkcia sa používa na reprezentáciu derivácií v diferenciálnych rovniciach. Ale v tomto prípade, aby sa zobrazila závislosť funkcie od jej argumentu, je napísaná ako „diff(f(x), x) a samotná funkcia je f(x).
Príklad. Nájdite všeobecné riešenie obyčajnej diferenciálnej rovnice prvého rádu y" - ax = 0.

Ak je hodnota pravej strany rovnice nula, potom ju možno úplne vynechať. Prirodzene, pravá strana rovnice môže obsahovať výraz.
Ako vidíte, pri riešení diferenciálnych rovníc Maxima používa integračnú konštantu %c, čo je z matematického hľadiska ľubovoľná konštanta určená z dodatočných podmienok.
Existuje ďalší spôsob riešenia bežnej diferenciálnej rovnice, ktorý je pre používateľa jednoduchší. Za týmto účelom spustite príkaz Rovnice > Vyriešiť ODE a do okna Vyriešiť ODE zadajte argumenty funkcie ode2.

Maxima vám umožňuje riešiť diferenciálne rovnice druhého rádu. Slúži na to aj funkcia ode2. Na označenie derivácií v diferenciálnych rovniciach sa používa funkcia diff, v ktorej sa pridáva ešte jeden argument - poradie rovnice: "diff(f(x), x, 2). Napríklad riešenie obyčajnej sekundovej- diferenciálna rovnica poriadku a·y"" + b·y" = 0 bude vyzerať takto:

Spolu s funkciou ode2 môžete použiť tri funkcie, ktorých použitie vám umožňuje nájsť riešenie za určitých obmedzení na základe všeobecného riešenia diferenciálnych rovníc získaných funkciou ode2:
- ic1 (výsledok funkcie ode2, počiatočná hodnota nezávisle premennej v tvare x = x 0, hodnota funkcie v bode x 0 v tvare y = y 0). Navrhnuté na riešenie diferenciálnej rovnice prvého poriadku s počiatočnými podmienkami.
- ic2(výsledok funkcie ode2, počiatočná hodnota nezávisle premennej v tvare x = x 0, hodnota funkcie v bode x 0 v tvare y = y 0, počiatočná hodnota pre prvú deriváciu závislej premennej vzhľadom na nezávisle premenná v tvare (y,x) = dy 0). Navrhnuté na riešenie diferenciálnej rovnice druhého rádu s počiatočnými podmienkami
- bc2(výsledok funkcie ode2, počiatočná hodnota nezávisle premennej v tvare x = x 0, hodnota funkcie v bode x 0 v tvare y = y 0, konečná hodnota nezávisle premennej v tvare x = x n, hodnota funkcie v bode x n v tvare y = y n). Navrhnuté na riešenie okrajového problému pre diferenciálnu rovnicu druhého rádu.
Podrobnú syntax týchto funkcií nájdete v dokumentácii systému.
Vyriešme Cauchyho úlohu pre rovnicu prvého rádu y" - ax = 0 s počiatočnou podmienkou y(n) = 1.

Uveďme príklad riešenia okrajovej úlohy pre diferenciálnu rovnicu druhého rádu y""+y=x s počiatočnými podmienkami y(o) = 0; y(4)=1.

Treba mať na pamäti, že systém často nedokáže vyriešiť diferenciálne rovnice. Napríklad, keď sa snažíme nájsť všeobecné riešenie bežnej diferenciálnej rovnice prvého rádu, dostaneme:

V takýchto prípadoch Maxima buď vydá chybové hlásenie (ako v tomto príklade), alebo jednoducho vráti „false“.
Ďalšia možnosť riešenia bežných diferenciálnych rovníc prvého a druhého rádu je navrhnutá na nájdenie riešení s počiatočnými podmienkami. Implementuje sa pomocou funkcie desolve.
Syntax funkcie:
desolve(diferenciálna rovnica, premenná);
Ak sa rieši systém diferenciálnych rovníc alebo existuje niekoľko premenných, rovnica a/alebo premenné sú prezentované vo forme zoznamu:
desolve([zoznam rovníc], [premenná1, premenná2,...]);
Rovnako ako v predchádzajúcej verzii sa na označenie derivácií v diferenciálnych rovniciach používa funkcia diff, ktorá má tvar „diff(f(x), x).
Počiatočné hodnoty pre premennú poskytuje funkcia atvalue. Táto funkcia má nasledujúcu syntax:
atvalue(funkcia, premenna = bod, hodnota v bode);
V tomto prípade sa predpokladá, že hodnoty funkcií a (alebo) ich derivátov sú nastavené na nulu, takže syntax funkcie hodnoty je:
atvalue(funkcia, premenna = 0, hodnota v bode "0");
Príklad. Nájdite riešenie diferenciálnej rovnice prvého rádu y"=sin(x) s počiatočnou podmienkou.

Všimnite si, že aj keď neexistuje žiadna počiatočná podmienka, funkcia bude tiež fungovať a vytvorí výsledok:

To umožňuje testovať riešenie na konkrétnu počiatočnú hodnotu. Skutočne, dosadením hodnoty y(0) = 4 do výsledného výsledku dostaneme y(x) = 5 - cos(x).
Funkcia desolve umožňuje riešiť sústavy diferenciálnych rovníc s počiatočnými podmienkami.
Uveďme príklad riešenia sústavy diferenciálnych rovníc  s počiatočnými podmienkami y(0) = 0; z(0) = 1.
s počiatočnými podmienkami y(0) = 0; z(0) = 1.

Spracovanie dát
Štatistická analýza
Systém umožňuje vypočítať základné štatistické popisné štatistiky, pomocou ktorých sú popísané najvšeobecnejšie vlastnosti empirických údajov. Základné popisné štatistiky zahŕňajú priemer, rozptyl, smerodajnú odchýlku, medián, modus, maximálne a minimálne hodnoty, rozsah variácie a kvartily. Schopnosti Maximy sú v tomto ohľade trochu skromné, ale väčšina týchto štatistík sa s jej pomocou dá celkom ľahko vypočítať.
Najjednoduchší spôsob výpočtu štatistickej popisnej štatistiky je použiť paletu Štatistika.

Panel obsahuje množstvo nástrojov zoskupených do štyroch skupín.
- Štatistické ukazovatele (opisná štatistika):
- priemer (aritmetický priemer);
- medián (medián);
- rozptyl (variance);
- odchýlka (štandardná odchýlka).
- Testy.
- Konštrukcia piatich typov grafov:
- histogram. Používa sa predovšetkým v štatistike na zobrazenie intervalových radov rozdelení. Počas jeho konštrukcie sú časti alebo frekvencie vynesené pozdĺž osi y a hodnoty atribútov sú vynesené na osi x;
- bodový graf (korelačný diagram, korelačné pole, Scatter Plot) - graf bodov, keď sa body nespájajú. Používa sa na zobrazenie údajov pre dve premenné, z ktorých jedna je faktorom a druhá výsledkom. S jeho pomocou sa vykonáva grafické znázornenie párov údajov vo forme množiny bodov („oblakov“) na súradnicovej rovine;
- Stĺpcový graf - graf vo forme zvislých stĺpcov;
- sektorový alebo koláčový graf (Pie Chart). Takýto diagram je rozdelený do niekoľkých segmentov - sektorov, z ktorých plocha každého je úmerná ich časti;
- box plot (krabica s fúzom, krabica s fúzom, krabicový graf, krabicový diagram). Je to ten, ktorý sa najčastejšie používa na zobrazenie štatistických údajov. Informácie v tejto tabuľke sú veľmi informatívne a užitočné. Súčasne zobrazuje niekoľko hodnôt, ktoré charakterizujú sériu variácií: minimálne a maximálne hodnoty, priemer a medián, prvý a tretí kvartil.
- Nástroje na čítanie alebo vytváranie matice. Ak chcete použiť nástroje palety, musíte mať počiatočné údaje vo forme matice - jednorozmerného poľa. Môžete ho vytvoriť v dokumente s aktuálnou reláciou a následne nahradiť jeho názov ako vstup v oknách nástrojov palety rovnakým spôsobom ako pri riešení rovníc pomocou panela General Math. Údaje môžete zadať aj priamo do okien na zadávanie vstupných údajov. V tomto prípade sa zadávajú vo forme akceptovanej v systéme, teda v hranatých zátvorkách a oddelené čiarkami. Je zrejmé, že prvá možnosť je oveľa lepšia, pretože vyžaduje iba jednorazové zadanie údajov.
Okrem panela je možné pomocou príslušných funkcií použiť aj všetky štatistické nástroje.
Maxima- počítačový systém, ktorý umožňuje pracovať so symbolickými a číselnými výrazmi. Podporuje operácie sériovej expanzie, diferenciácie, Laplaceovej transformácie, integrácie. Program sa nebojí obyčajných diferenciálnych rovníc, matíc a tenzorov, sústav lineárnych rovníc, zoznamov, vektorov, polynómov, množín. Počítačový výpočtový systém dokáže vytvárať výpočty s vysokým stupňom presnosti. Používa celé čísla a zlomkové výrazy. Aplikácia dokáže vytvárať grafy v dvoch alebo troch rozmeroch. Má manuál, ktorý podrobne popisuje, ako pracovať s nástrojom, ktoré operátory sú podporované systémom matematických operácií. Program je ideálny pre milovníkov počítačovej algebry: študentov, učiteľov, postgraduálnych študentov.


- Pracuje s matematickými číselnými a symbolickými výrazmi.
- Podporuje prácu so zoznamami, polynómami, maticami, tenzormi, diferenciálnymi rovnicami a sústavami lineárnych rovníc.
- Podporuje operácie sériovej expanzie, diferenciácie, Laplaceovej transformácie, integrácie.
- Vykonáva výpočty s vysokým stupňom presnosti.
- Používa celé čísla, zlomkové výrazy.
- Schopný vytvárať grafy v dvojrozmerných alebo trojrozmerných rozmeroch.
- Vhodné pre fanúšikov počítačovej algebry.
- Má prístupnú dokumentáciu na oboznámenie sa s prevádzkou systému.
- Neovplyvňuje výkon a rýchlosť operačného prostredia.
- Existuje podpora pre ruský jazyk.
Nevýhody programu
- Neexistuje žiadna prenosná verzia.- Procesor s taktovacou frekvenciou 1200 MHz alebo výkonnejší.
- RAM 256 MB alebo viac.
- Voľné miesto na pevnom disku od 185 MB.
- 32-bitová alebo 64-bitová architektúra (x86 alebo x64).
- Operačný systém Windows XP, Windows Vista, Windows 7, Windows 8
Multifunkčné kalkulačky: Porovnávacie tabuľky
| Názov programu | V ruštine | Distribúcie | Inštalátor | Popularita | Veľkosť | Index |
| ★ ★ ★ ★ ★ | 48,7 MB | 100 | ||||
| ★ ★ ★ ★ ★ | 59,8 MB | 99 | ||||
| ★ ★ ★ ★ ★ | 1,3 MB | 86 | ||||
Systém Maxima má mnoho vstavaných funkcií. Každá vstavaná funkcia môže byť popísaná v dokumentácii obsiahnutej v systéme pomoci. Pomocník je prístupný pomocou funkčného klávesu F1. Maxima má aj špeciálnu funkciu, ktorá poskytuje informácie z dokumentácie pre konkrétne slová. Skrátená verzia tohto volania funkcie: ?? názov (obr. 12). Tu?? je názov operátora a argument musí byť od neho oddelený medzerou. Operátor?? zobrazí zoznam tých častí pomocníka a názvov funkcií, ktoré obsahujú zadaný text, a potom vás vyzve na zadanie čísla časti alebo popisu funkcie, ktorú si chcete pozrieť:
Obr. 12. Volanie pomoci na systémový príkaz Maxima, ktorý vás zaujíma
Všimnite si, že v systéme Maxima neexistuje jasný rozdiel medzi operátormi a funkciami. navyše každý príkaz je vlastne funkcia.
Všetky funkcie a operátory Maxima pracujú nielen s reálnymi číslami, ale aj s číslami komplexnými. Samotné komplexné čísla sú zapísané v algebraickej forme, pričom imaginárna jednotka je označená %i; teda v tvare a+b*%i, kde A A b sú skutočné a imaginárne časti čísla, resp.
Uvažujme syntax základnej funkcie Systémy Maxima.
1. Aritmetické operátory: + , -, *, /, -->. Príklad:

3. Logické operátory: a, alebo, nie. Príklad:

4. Funkcia na nájdenie faktoriálu čísla: !
Faktoriál je daný v najvšeobecnejšom tvare a je to v skutočnosti funkcia gama (presnejšie x! = gama(x+1)), to znamená, že je definovaná na množine všetkých komplexných čísel okrem záporných celých čísel. Faktoriál prirodzeného čísla (a nuly) sa automaticky zjednoduší na rovnaké prirodzené číslo.
![]()
5. Funkcia na nájdenie semifaktoriálu je: !! (súčin všetkých párnych (pre párny operand) alebo nepárnych čísel menších alebo rovných danému).
6. Funkcia negácie syntaktickej rovnosti: # Zápis a#b je ekvivalentný s nie a=b. 
7. Funkcia na nájdenie modulu čísla x: abs(x) Modul je definovaný pre všetky komplexné čísla. Príklad:

8. Funkcia, ktorá vracia znamienko čísla x: signum(x)

9. Funkcie, ktoré vracajú najväčšie a najmenšie hodnoty daných reálnych čísel: max(x1,...,xn) a min(x1,...,xn).

10. Niektoré vstavané matematické funkcie:
| sqrt(x) | Druhá odmocnina z x |
| acos(x) | Arkosínus argumentu x |
| Acosh (x) | Hyperbolický oblúk kosínus x |
| acot(x) | Arkotangens argumentu x |
| acoth (x) | Hyperbolický oblúk kotangens argumentu x |
| acsc(x) | Arkosekansa argumentu x |
| acsch(x) | Hyperbolický arkosekans argumentu x |
| asec(x) | Arkásekans argumentu x |
| asech(x) | Hyperbolický arcsekans argumentu x |
| asin(x) | Arkásína argumentu x |
| asinh(x) | Hyperbolický arkussínus argumentu x |
| atan(x) | Arkustangens argumentu x |
| atanh (x) | Hyperbolický arkustangens argumentu x |
| cosh(x) | Hyperbolický kosínus argumentu x |
| coth(x) | Hyperbolický kotangens argumentu x |
| csc(x) | Kosekans argumentu x |
| csch(x) | Hyperbolický kosekans argumentu x |
| sek(x) | Sekans argumentu x |
| sech(x) | Hyperbolický sekans argumentu x |
| hriech(x) | Sínus x |
| sinh(x) | Hyperbolický sínus argumentu x |
| tan(x) | Tangenta x |
| tanh(x) | Hyperbolický tangens argumentu x |
| log(x) | Prirodzený logaritmus x |
| exp(x) | Exponent x |
11. Funkcie pre prácu s maticami:
determinant – nájdenie determinantu matice:
vlastné hodnoty – nájdenie vlastných hodnôt matice:
prevrátiť- získanie inverznej matice:

maloletý– definuje moll matice. Prvý argument je matica, druhý a
tretím sú indexy riadkov a stĺpcov:
hodnosť- poradie matice:
submatice– vráti matricu získanú z originálu odstránením
zodpovedajúce riadky a/alebo stĺpce. Parametre sú:
počty riadkov, ktoré sa majú vymazať, pôvodná matica, počty stĺpcov, ktoré sa majú vymazať.

transponovať- maticová transpozícia:

Systémový jazyk Maxima obsahuje základné spustiteľné operátory, ktoré sa nachádzajú v akomkoľvek programovacom jazyku. Pozrime sa na ne.
Operátory priraďovania hodnôt (názvové výrazy).
1. Operátor „:“ (operátor pre nastavenie hodnoty premennej).
2. Operátor „:=“ (operátor pre špecifikáciu užívateľskej funkcie).
3. Rozšírené verzie operátorov priradenia a priradenia funkcií, označené ako:: a::=.
Použitie operátora používateľskej sady funkcií výrazne uľahčuje prácu s ním, pretože ho môžete odkázať na meno a jednoducho a pohodlne vypočítať hodnoty funkcií v daných bodoch.
Príklad: nájdite hodnotu funkcie f (x, y)=cosx + hriech r v bode

Operátor slučky. Operátor slučky môže byť špecifikovaný niekoľkými spôsobmi. Spôsob určenia závisí od toho, či je vopred známe, koľkokrát je potrebné vykonať telo cyklu.
Príklad: Nastavenie slučky na zobrazenie hodnôt premennej A v rozsahu od -3 do 10 v krokoch po 5:

Ďalšou dôležitou vlastnosťou systému Maxima je práca so zoznamami a poliami.
Na generovanie zoznamov použite príkaz makelist. Napríklad pomocou príkazu

vytvorili sme zoznam s názvom x, pozostávajúci z desiatich prvkov, ktorých hodnoty sa nachádzajú podľa vzorca.
Ak chcete vytvoriť polia, použite príkaz pole. Napríklad pomocou príkazu
![]()
vytvorili sme dvojrozmerné pole A pozostávajúce z 10 riadkov a 5 stĺpcov. Na vyplnenie poľa prvkami použijeme slučku s parametrom. Napríklad,
Na zobrazenie prvkov poľa na obrazovke môžete použiť príkaz:
Pole môže byť vytvorené bez predchádzajúcej deklarácie. V nasledujúcom príklade sme vytvorili jednorozmerné pole x pozostávajúce z 5 prvkov, ktorých hodnoty sa vypočítajú pomocou vzorca x( i)=hriech i

Nevýhoda práce s poľami spočíva v tom, že hodnoty prvkov poľa sú zobrazené v stĺpci. Je oveľa pohodlnejšie, ak sú hodnoty (dvojrozmerného) poľa zobrazené ako matica. Na tieto účely môžete použiť príkaz genmatrix. Ak chcete napríklad vygenerovať dvojrozmerné pole (maticu), mali by ste zadať príkaz v nasledujúcom tvare:
Vypíšme výsledné pole:

6. Najjednoduchšie premeny výrazov.
Štandardne je v systéme Maxima aktívna funkcia Autosimplification, t.j. systém sa sám bez príkazu snaží zjednodušiť zadaný výraz.
Príklad. Predpokladajme, že potrebujete nájsť hodnotu nasledujúceho číselného výrazu:
Nastavme výraz podľa pravidiel systémového jazyka Maxima.

Ako vidíte, systém odpovedal hodnotou výrazu, aj keď sme nezadali žiadny príkaz.
Ako môžete prinútiť systém, aby nevydával výsledok, ale samotný výraz? Aby ste to dosiahli, musíte deaktivovať funkciu zjednodušenia pomocou príkazu simp: false$. Potom dostaneme:

Ak chcete aktivovať funkciu zjednodušenia, musíte zadať príkaz simp:true$. Funkcia autosimplify môže pracovať s numerickými aj niektorými nenumerickými výrazmi. Napríklad,

Pri zadávaní môžeme odkazovať na ktorúkoľvek z predchádzajúcich buniek jej názvom, pričom ju nahrádzame v ľubovoľných výrazoch. Okrem toho je posledná výstupná bunka označená % a posledná vstupná bunka je označená _. To vám umožní odkázať na posledný výsledok bez toho, aby vás rozptyľovalo jeho číslo. Takéto volania do buniek by sa však nemali zneužívať, pretože pri prehodnocovaní celého dokumentu alebo jeho jednotlivých vstupných buniek môže dôjsť k nesúladu medzi číslami buniek.
Príklad. Nájdite hodnotu výrazu a zvýšte výsledok 5-krát.

Namiesto názvov buniek je vhodné použiť premenné a ich názvy priradiť ľubovoľným výrazom. V tomto prípade môže ako hodnota premennej pôsobiť akýkoľvek matematický výraz.
Hodnoty názvov premenných sú zachované počas celej práce s dokumentom. Pripomeňme si, že ak je potrebné odstrániť definíciu z premennej, možno to urobiť pomocou funkcie kill(name), kde name je názov výrazu, ktorý sa má zničiť; navyše to môže byť buď vami priradený názov, alebo akákoľvek vstupná alebo výstupná bunka. Podobne môžete vymazať celú pamäť a uvoľniť všetky mená zadaním príkazu kill(all) (alebo výberom ponuky Machta->Vymazať pamäť(Vymazať pamäť)). V tomto prípade sa tiež vymažú všetky I/O bunky a ich číslovanie bude opäť začínať od jednej.
Funkcia autosimplify nie vždy dokáže zjednodušiť výraz. Okrem nej existuje množstvo príkazov, ktoré sú určené na prácu s výrazmi: racionálne a iracionálne. Pozrime sa na niektoré z nich.
krysa (výraz) - transformuje racionálny výraz na kanonickú formu: otvorí všetky zátvorky, potom všetko uvedie do spoločného menovateľa, sčíta a zredukuje; prevedie všetky čísla v konečnej desatinnej sústave na racionálne čísla. Kanonická forma je automaticky „zrušená“ v prípade akýchkoľvek transformácií, ktoré nie sú racionálne
ratsimp (výraz) - zjednodušuje výraz prostredníctvom racionálnych premien. Funguje to aj „do hĺbky“, to znamená, že iracionálne časti výrazu sa nepovažujú za atómové, ale všetky racionálne prvky v nich sú zjednodušené.
fullratsimp(expression) - funkcia na zjednodušenie racionálneho výrazu postupnou aplikáciou funkcie ratsimp() na odovzdaný výraz. Vďaka tomu je funkcia o niečo pomalšia ako ratsimp(), ale poskytuje spoľahlivejší výsledok.
expand (výraz) - rozbalí zátvorky vo výraze na všetkých úrovniach vnorenia. Na rozdiel od funkcie ratexpand() neredukuje zlomky na spoločného menovateľa.
radcan(výraz) - funkcia na zjednodušenie logaritmických, exponenciálnych a mocninných funkcií s neceločíselnými racionálnymi exponentmi, teda koreňmi (radikálmi).
Často, keď sa pokúsite zjednodušiť výraz v Maxime, môže to v skutočnosti len urobiť zložitejším. K zvýšeniu výsledku môže dôjsť v dôsledku skutočnosti, že nie je známe, aké hodnoty môžu mať premenné zahrnuté vo výraze. Aby ste tomu zabránili, mali by ste obmedziť hodnoty, ktoré môže premenná nadobudnúť. To sa vykonáva pomocou funkcie predpokladať (podmienka). Preto v niektorých prípadoch možno najlepší výsledok dosiahnuť kombináciou radcan() s ratsimp() alebo fullratsimp().