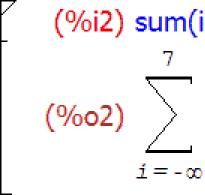Максималды сипаттама. Максимуммен қалай жұмыс істеу керек
Maxima математикалық пакеті MathCAD үшін ең жақсы тегін ауыстырулардың бірі болып табылады.
Бұл оқу құралын (pdf форматында) егер мемлекеттік білім беру стандартында «Дифференциалдық дифференциалдық» бөлімін оқу қарастырылған болса, жоғары кәсіптік оқу орындарында әртүрлі мамандықтар бойынша математикалық талдау, дифференциалдық теңдеулер, қолданбалы бағдарламалық кешен және т.б. Теңдеулер», сондай-ақ элективті курстарда. Сондай-ақ математика мен информатиканы тереңдетіп оқытатын жалпы білім беретін мекемелердің бейіндік сыныптарында компьютерлік математика жүйелерімен танысу үшін де пайдалы болуы мүмкін.
- Алғы сөз
- 1-тарау. Maxima компьютерлік математика жүйесінде жұмыс істеу негіздері
- 1.1. Maxima жүйесі туралы
- 1.2. Жеке компьютерге Maxima орнату
- 1.3. Maxima негізгі терезе интерфейсі
- 1.4. Максимадағы ұяшықтармен жұмыс
- 1.5. Maxima анықтамалық жүйесімен жұмыс
- 1.6. Maxima жүйесінің функциялары мен командалары
- 1.7. Максимада есептеу процесін басқару
- 1.8. Қарапайым өрнек түрлендірулері
- 1.9. Алгебралық теңдеулер және олардың жүйелерін шешу
- 1.10. Графикалық мүмкіндіктер
- 2-тарау. Дифференциалдық теңдеулерді шешудің сандық әдістері
- 2.1. Дифференциалдық теңдеулер туралы жалпы мәліметтер
- 2.2. Бірінші ретті қарапайым дифференциалдық теңдеу үшін Коши есебін шешудің сандық әдістері
- 2.2.1. Эйлер әдісі
- 2.2.2. Эйлер-Коши әдісі
- 2.2.3. Рунге-Кутта әдісі 4 реттік дәлдік
- 2.3. Қарапайым дифференциалдық теңдеулер үшін шекті есептерді ақырлы айырым әдісімен шешу
- 2.4. Дербес дифференциалдық теңдеулерді шешудің тор әдісі
- 3 тарау. Maxima жүйесінде дифференциалдық теңдеулердің шешімін табу
- 3.1. Дифференциалдық теңдеулердің шешімдерін табуға арналған кіріктірілген функциялар
- 3.2. Дифференциалдық теңдеулер және олардың жүйелерін символдық түрде шешу
- 3.3. Дифференциалдық теңдеулердің траекториялары мен бағыт өрістерін құру.
- 3.4. Қарапайым дифференциалдық теңдеулер үшін Коши есебін шешудің сандық әдістерін жүзеге асыру
- 3.4.1. Эйлер әдісі
- 3.4.2. Эйлер-Коши әдісі
- 3.4.3. Рунге-Кутта әдісі
- 3.5. Қарапайым дифференциалдық теңдеулер үшін шекті есептерді шешудің ақырлы айырымы әдісін жүзеге асыру
- 3.6. Дербес дифференциалдық теңдеулер үшін тор әдісін жүзеге асыру
- Өз бетінше шешуге арналған тапсырмалар
- Әдебиет
Алғы сөз
Дифференциалдық теңдеулер теориясы қазіргі математиканың ең үлкен салаларының бірі болып табылады. Дифференциалдық теңдеулердің негізгі ерекшеліктерінің бірі – дифференциалдық теңдеулер теориясы мен қолданбалы салалардың тікелей байланысы. Кез келген физикалық құбылысты зерттегенде зерттеуші, ең алдымен, оның математикалық идеализациясын немесе математикалық моделін жасайды, осы құбылысты реттейтін негізгі заңдылықтарды математикалық формада жазады. Көбінесе бұл заңдар дифференциалдық теңдеулер түрінде көрсетілуі мүмкін. Бұл континуум механикасының әртүрлі құбылыстарының, химиялық реакциялардың, электрлік және магниттік құбылыстардың және т.б. модельдер болып шығады. Алынған дифференциалдық теңдеулерді, әдетте, бастапқы және шекаралық шарттар түрінде нақтыланатын қосымша шарттармен бірге зерттеу арқылы , математик болып жатқан құбылыс туралы ақпарат алады, кейде оның өткені мен болашағын біле алады.
Математикалық модельді дифференциалдық теңдеулер түрінде құрастыру үшін, әдетте, тек жергілікті байланыстарды білу керек және тұтас физикалық құбылыс туралы ақпарат қажет емес. Математикалық модель құбылысты тұтастай зерттеуге, оның дамуын болжауға және уақыт бойынша ондағы болатын өлшемдерге сапалы баға беруге мүмкіндік береді. Дифференциалдық теңдеулерді талдау негізінде электромагниттік толқындар ашылды.
Механиканың қажеттіліктері үшін дифференциалдық теңдеулерді шешу қажеттілігі, яғни қозғалыс траекторияларын табу өз кезегінде Ньютонның жаңа есептеулерді жасауға түрткі болды деп айта аламыз. Жаңа есептеулерді геометрия мен механика есептеріне қолдану қарапайым дифференциалдық теңдеулер арқылы жасалды.
Есептеуіш техниканың заманауи дамуы мен жаңа бағыт – компьютерлік математиканың қарқынды дамуын ескере отырып, компьютерлік математика жүйелері деп аталатын программалық пакеттер кең таралып, сұранысқа ие болды.
Компьютерлік математика – іргелі математиканың, ақпараттық және компьютерлік технологиялардың тоғысында пайда болған ғылым мен білімнің жаңа бағыты. Компьютерлік математика жүйесі (SCM) – арнайы жасалған тілде шарттарды көрсету кезінде математикалық есептерді автоматтандырылған, технологиялық біртұтас және тұйық циклде өңдеуді қамтамасыз ететін бағдарламалар жиынтығы.
Заманауи компьютерлік математикалық жүйелер көп терезелі графикалық интерфейсі бар және оларды үйрену мен пайдалануды жеңілдететін дамыған анықтамалық жүйесі бар бағдарламалар. SCM дамуының негізгі тенденциялары математикалық мүмкіндіктердің өсуі, әсіресе аналитикалық және символдық есептеулер саласында, есептеулердің барлық кезеңдері үшін визуализация құралдарының айтарлықтай кеңеюі, 2D және 3D графикасын кеңінен қолдану, әртүрлі технологияларды біріктіру болып табылады. жүйелердің бір-бірімен және басқа бағдарламалық қамтамасыз етумен, Интернетке кең қол жетімділікпен, Интернеттегі оқу және ғылыми жобалар бойынша ынтымақтастықты ұйымдастыру, анимация және кескіндерді өңдеу құралдарын, мультимедиялық құралдарды және т.б.
Соңғы кезге дейін білім беруде SCM-ді кеңінен қолдануға кедергі келтірген маңызды жағдай кәсіби ғылыми математикалық бағдарламалық қамтамасыз етудің жоғары құны болып табылады. Дегенмен, соңғы уақытта мұндай бағдарламаларды әзірлейтін және тарататын көптеген компаниялар (Интернет арқылы - http://www.softline.ru) өздерінің бағдарламаларының бұрынғы нұсқаларын тегін пайдалануға ұсынады, оқу орындарына жеңілдіктер жүйесін кеңінен қолданады және демонстрацияларды таратады. тегін бағдарламаларға арналған сынақ нұсқалары
Сонымен қатар, компьютерлік математикалық жүйелердің тегін аналогтары пайда болады, мысалы, Maxima, Scilab, Octave және т.б.
Бұл оқулық дифференциалдық теңдеулердің шешімдерін табу үшін Maxima компьютерлік математика жүйесінің мүмкіндіктерін зерттейді.
Неліктен Максима?
Біріншіден, Maxima жүйесі коммерциялық емес ашық бастапқы жоба болып табылады. Maxima GNU GPL (General Public License) бойынша таратылатын бағдарламалық өнімдер класына жатады.Екіншіден, Maxima – математикалық есептерді сандық және символдық түрде шешуге арналған бағдарлама. Оның мүмкіндіктерінің ауқымы өте кең: өрнектерді түрлендіру әрекеттері, өрнек бөліктерімен жұмыс, сызықтық алгебра есептерін шешу, математикалық анализ, комбинаторика, сандар теориясы, тензорлық талдау, статистикалық есептер, жазықтықта және кеңістікте функциялардың графиктерін тұрғызу. әртүрлі координаттар жүйесінде және т.б. d.
Үшіншіден, Maxima-да WxMaxima (http://wxmaxima.sourceforge.net) деп аталатын қуатты, тиімді және пайдаланушыға ыңғайлы кросс-платформалық графикалық интерфейсі бар.
Кітап авторлары он жыл бойы Mathematica, Maple, MathCad сияқты компьютерлік математика жүйелерін зерттеп келеді. Сондықтан осы бағдарламалық өнімдердің мүмкіндіктерін біле отырып, атап айтқанда дифференциалдық теңдеулердің шешімін табу үшін еркін таратылатын компьютерлік математикалық жүйелерде символдық түрдегі есептеулерді ұйымдастыруға байланысты мәселені зерттегім келді.
Бұл нұсқаулықта Maxima жүйесі негізінде дифференциалдық теңдеулердің шешімдерін іздеу процесін ұйымдастыру мүмкіндіктері туралы айтылады және жүйеде жұмысты ұйымдастыру туралы жалпы ақпарат бар.
Нұсқаулық 3 тараудан тұрады. Бірінші тарауда оқырмандарды Maxima жүйесінің wxMaxima графикалық интерфейсі, ондағы жұмыс істеу мүмкіндіктері және жүйелік тілдің синтаксисі таныстырады. Жүйені қарастыру жүйенің таралуын қайдан табуға болатынынан және оны орнату жолынан басталады. Екінші тарауда дифференциалдық теңдеулер теориясының жалпы мәселелері және оларды шешудің сандық әдістері қарастырылады.
Үшінші тарау 1-ші және 2-ші ретті қарапайым дифференциалдық теңдеулердің шешімдерін символдық түрде табуға арналған Maxima компьютерлік математика жүйесінің кірістірілген функцияларына арналған. Сондай-ақ үшінші тарауда Maxima жүйесінде дифференциалдық теңдеулерді шешудің сандық әдістерінің орындалуы көрсетілген. Нұсқаулықтың соңында өз бетінше шешуге арналған тапсырмалар берілген.
Пайдаланушылардың кең ауқымы нұсқаулыққа қызығушылық танытады және ол математикалық есептерді шешудің жаңа құралын меңгеруде олардың көмекшісі болады деп үміттенеміз.
Т.Н. Губина, Е.В. Андропова
Елец, шілде 2009 ж
P.S. Жылдам бастау: командаларды орындау үшінжәне mwMaxima-дағы функциялар үшін алдымен пәрменнің өзін енгізу керек, содан кейін crtl+Enter пернелерін басыңыз.
Математикалық талдау операциялары
Сомалар
Қосындыны табу үшін қосынды функциясы қолданылады. Функция синтаксисі:
қосынды(өрнек, айнымалы, айнымалы өзгерістің төменгі шегі, айнымалы өзгерістің жоғарғы шегі)
Мысалы:
Соңғы аргументке оң шексіздік «inf» жүйелік айнымалы мәнін тағайындасаңыз, бұл жоғарғы шекараның жоқтығын көрсетеді және шексіз қосынды есептеледі. Сондай-ақ, теріс шексіздік жүйесінің айнымалысы «minf» мәнін «айнымалы өзгерісінің төменгі шегі» аргументіне тағайындасаңыз, шексіз сома есептеледі. Дәл осындай мәндер басқа математикалық талдау функцияларында қолданылады.
Мысалы:

Жұмыстар
Ақырлы және шексіз туындыларды табу үшін туынды функциясын пайдаланыңыз. Оның қосынды функциясы сияқты аргументтері бар.
Мысалы:

Шектеулер
Шектерді табу үшін шектеу функциясын пайдаланыңыз.
Функция синтаксисі:
шектеу (өрнек, айнымалы, тоқтау нүктесі)
Егер «үзіліс нүктесі» аргументі «inf» мәніне орнатылса, бұл шекараның жоқтығын көрсетеді.
Мысалы:

Бір жақты шектеулерді есептеу үшін оң жақтағы шектеулерді есептеу үшін плюс және сол жақта минус мәні бар қосымша аргумент қолданылады.
Мысалы, arctan(1/(x - 4)) функциясының үзіліссіздігін зерттейік. Бұл функция x = 4 нүктесінде анықталмаған. Оң және сол жақтағы шектерді есептейік:

Көріп отырғанымыздай, х = 4 нүктесі осы функция үшін бірінші текті үзіліс нүктесі болып табылады, өйткені сол және оң жақта шекаралар бар, олар сәйкесінше -PI/2 және PI/2-ге тең.
Дифференциалдар
Дифференциалдарды табу үшін дифференциал функциясы қолданылады. Функция синтаксисі:
diff(өрнек, айнымалы1, айнымалы1 үшін туынды реті [,айнымалы2, айнымалы2 үшін туынды реті,...])
мұндағы өрнек дифференциалданатын функция болса, екінші аргумент – оған қатысты туынды алынуы тиіс айнымалы, үшінші (міндетті емес) – туындының реті (әдепкі бойынша – бірінші рет).
Мысалы:

Жалпы, дифференция функциясы үшін тек бірінші аргумент қажет. Бұл жағдайда функция өрнектің дифференциалын қайтарады. Сәйкес айнымалының дифференциалы del(айнымалы атауы) арқылы белгіленеді:

Функцияның синтаксисінен көріп отырғанымыздай, пайдаланушының бір уақытта бірнеше дифференциалдау айнымалыларын анықтау және олардың әрқайсысы үшін ретті орнату мүмкіндігі бар:

Параметрлік функцияны пайдалансаңыз, функцияның жазылу формасы өзгереді: функция атынан кейін «:=» таңбалары жазылады, ал функцияға оның аты арқылы параметр арқылы қол жеткізіледі:

Туындыны берілген нүктеде есептеуге болады. Бұл келесідей орындалады:

Дифф функциясы төменде қарастырылғандай, дифференциалдық теңдеулерде туындыларды белгілеу үшін де қолданылады.
Интегралдар
Жүйедегі интегралдарды табу үшін интегралдау функциясын пайдаланыңыз. Функцияның анықталмаған интегралын табу үшін екі аргумент қолданылады: функцияның аты және интегралдау жүзеге асырылатын айнымалы. Мысалы:

Егер жауап түсініксіз болса, Максима қосымша сұрақ қоюы мүмкін:
Жауапта сұрақтың мәтіні болуы керек. Бұл жағдайда у айнымалысының мәні «0-ден» үлкен болса, ол «оң», ал басқа жағдайда «теріс» болады. Бұл жағдайда сөздің бірінші әрпін ғана енгізуге болады.
Функцияда анықталған интегралды табу үшін қосымша аргументтерді көрсету керек: интегралдың шектері:
Maxima сонымен қатар шексіз интеграциялық шектеулерге мүмкіндік береді. Мұны істеу үшін функцияның үшінші және төртінші аргументтері үшін «-inf» және «inf» мәндері пайдаланылады:

Интегралдың жуық мәнін сандық түрде табу үшін, бұрын айтылғандай, сіз шығыс ұяшығынан нәтижені таңдап, ондағы контекстік мәзірге қоңырау шалып, одан «Қалқылау» тармағын таңдаңыз (жылжымалы нүкте нөміріне түрлендіру) .

Жүйе сонымен қатар бірнеше интегралды есептеуге қабілетті. Бұл әрекетті орындау үшін, біріктіру функциялары бір-біріне кірістірілген. Төменде қос анықталмаған интегралды және қос анықталған интегралды есептеу мысалдары берілген:

Дифференциалдық теңдеулердің шешімдері
Дифференциалдық теңдеулерді шешудегі мүмкіндіктері бойынша Максима, мысалы, Maple-дан айтарлықтай төмен. Бірақ Максима бәрібір қарапайым бірінші және екінші ретті дифференциалдық теңдеулерді, сондай-ақ олардың жүйелерін шешуге мүмкіндік береді. Ол үшін мақсатқа байланысты екі функция қолданылады. Қарапайым дифференциалдық теңдеулердің жалпы шешімі үшін ode2 функциясы, ал бастапқы шарттар негізінде теңдеулер немесе теңдеулер жүйесінің шешімдерін табу үшін шешу функциясы қолданылады.
ode2 функциясының келесі синтаксисі бар:
ode2(теңдеу, тәуелді айнымалы, тәуелсіз айнымалы);
Дифференциалдық теңдеулерде туындыларды көрсету үшін дифференциалды функция қолданылады. Бірақ бұл жағдайда функцияның аргументіне тәуелділігін көрсету үшін ол “diff(f(x), x) түрінде жазылады, ал функцияның өзі f(x).
Мысал. Кәдімгі бірінші ретті дифференциалдық у» теңдеудің жалпы шешімін табыңыз - ax = 0.

Егер теңдеудің оң жағының мәні нөлге тең болса, онда оны мүлдем алып тастауға болады. Әрине, теңдеудің оң жағында өрнек болуы мүмкін.
Көріп отырғаныңыздай, дифференциалдық теңдеулерді шешу кезінде Максима %c интегралдау константасын пайдаланады, ол математикалық тұрғыдан қосымша шарттардан анықталатын ерікті тұрақты болып табылады.
Кәдімгі дифференциалдық теңдеуді шешудің басқа жолы бар, ол пайдаланушыға оңайырақ. Ол үшін Equations > Solve ODE командасын орындаңыз және ODE шешу терезесіне ode2 функциясының аргументтерін енгізіңіз.

Maxima екінші ретті дифференциалдық теңдеулерді шешуге мүмкіндік береді. Ол үшін ode2 функциясы да қолданылады. Дифференциалдық теңдеулерде туындыларды белгілеу үшін дифференциалды функция қолданылады, оған тағы бір аргумент қосылады – теңдеудің реті: «дифф(f(x), x, 2). Мысалы, кәдімгі секундтың шешімі- a·y"" + b·y" = 0 ретті дифференциалдық теңдеуі келесідей болады:

ode2 функциясымен бірге сіз үш функцияны пайдалана аласыз, оларды пайдалану ode2 функциясымен алынған дифференциалдық теңдеулердің жалпы шешіміне негізделген белгілі шектеулер бойынша шешім табуға мүмкіндік береді:
- ic1 (ode2 функциясының нәтижесі, x = x 0 түріндегі тәуелсіз айнымалының бастапқы мәні, y = y 0 түріндегі x 0 нүктесіндегі функцияның мәні). Бастапқы шарттары бар бірінші ретті дифференциалдық теңдеуді шешуге арналған.
- ic2(ode2 функциясының нәтижесі, x = x 0 түріндегі тәуелсіз айнымалының бастапқы мәні, y = y 0 түріндегі x 0 нүктесіндегі функцияның мәні, тәуелді айнымалының бірінші туындысы үшін бастапқы мәнге қатысты (y,x) = dy 0) түріндегі тәуелсіз айнымалы. Бастапқы шарттары бар екінші ретті дифференциалдық теңдеуді шешуге арналған
- bc2(ode2 функциясының нәтижесі, x = x 0 түріндегі тәуелсіз айнымалының бастапқы мәні, y = y 0 түріндегі x 0 нүктесіндегі функцияның мәні, x = x n түріндегі тәуелсіз айнымалының соңғы мәні, y = y n түріндегі x n нүктесіндегі функцияның мәні. Екінші ретті дифференциалдық теңдеу үшін шекаралық есепті шешуге арналған.
Бұл функциялардың егжей-тегжейлі синтаксисін жүйелік құжаттамадан табуға болады.
Бірінші ретті y" - ax = 0 теңдеуі үшін Коши есебін y(n) = 1 бастапқы шартымен шешейік.

Бастапқы шарттары y(o) = 0 болатын y""+y=x екінші ретті дифференциалдық теңдеу үшін шекаралық есепті шешуге мысал келтірейік; y(4)=1.

Жүйе жиі дифференциалдық теңдеулерді шеше алмайтынын есте ұстаған жөн. Мысалы, қарапайым бірінші ретті дифференциалдық теңдеудің жалпы шешімін табуға тырысқанда, біз мынаны аламыз:

Мұндай жағдайларда Maxima қате туралы хабарды шығарады (осы мысалдағыдай) немесе жай ғана "жалған" мәнін қайтарады.
Кәдімгі бірінші және екінші ретті дифференциалдық теңдеулерді шешудің тағы бір нұсқасы бастапқы шарттары бар шешімдерді табуға арналған. Ол шешу функциясы арқылы жүзеге асырылады.
Функция синтаксисі:
desolve(дифференциалдық теңдеу, айнымалы);
Егер дифференциалдық теңдеулер жүйесі шешілсе немесе бірнеше айнымалы болса, онда теңдеу және/немесе айнымалылар тізім түрінде ұсынылады:
desolve([теңдеулер тізімі], [айнымалы1, айнымалы2,...]);
Алдыңғы нұсқадағыдай, дифференциалдық теңдеулерде «diff(f(x), x) түріндегі туындыларды белгілеу үшін дифференциалды функция қолданылады.
Айнымалының бастапқы мәндері atvalue функциясы арқылы беріледі. Бұл функцияның келесі синтаксисі бар:
atvalue(функция, айнымалы = нүкте, нүктедегі мән);
Бұл жағдайда функциялардың және (немесе) олардың туындыларының мәндері нөлге тең болуы қарастырылады, сондықтан мәндік функцияның синтаксисі:
atvalue(функция, айнымалы = 0, "0" нүктесіндегі мән);
Мысал. y"=sin(x) бірінші ретті дифференциалдық теңдеудің бастапқы шарты бар шешімін табыңыз.

Бастапқы шарт болмаса да, функция жұмыс істеп, нәтиже беретінін ескеріңіз:

Бұл шешімді белгілі бір бастапқы мәнге сынауға мүмкіндік береді. Шынында да, алынған нәтижеге у(0) = 4 мәнін қойып, у(х) = 5 - cos(x) аламыз.
Desolve функциясы бастапқы шарттары бар дифференциалдық теңдеулер жүйесін шешуге мүмкіндік береді.
Дифференциалдық теңдеулер жүйесін шешуге мысал келтірейік  бастапқы шарттарымен y(0) = 0; z(0) = 1.
бастапқы шарттарымен y(0) = 0; z(0) = 1.

Мәліметтерді өңдеу
Статистикалық талдау
Жүйе негізгі статистикалық сипаттамалық статистиканы есептеуге мүмкіндік береді, оның көмегімен эмпирикалық деректердің ең жалпы қасиеттері сипатталады. Негізгі сипаттаушы статистикаға орташа, дисперсия, стандартты ауытқу, медиана, режим, максималды және ең аз мәндер, вариация диапазоны және квартилдер жатады. Осыған байланысты Максиманың мүмкіндіктері біршама қарапайым, бірақ бұл статистиканың көпшілігін оның көмегімен есептеу өте оңай.
Статистикалық сипаттамалық статистиканы есептеудің ең оңай жолы - Статистика палитрасын пайдалану.

Панельде төрт топқа топтастырылған бірнеше құралдар бар.
- Статистикалық көрсеткіштер (сипаттаушы статистика):
- орташа (орта арифметикалық);
- медиана(медиана);
- дисперсия (дисперсия);
- ауытқу (стандартты ауытқу).
- Тесттер.
- Графиктердің бес түрін құру:
- гистограмма. Ол ең алдымен статистикада таралулардың интервалдық қатарын бейнелеу үшін қолданылады. Оны құру кезінде ордината осі бойынша бөліктер немесе жиіліктер, ал абсцисса осінде атрибут мәндері сызылады;
- шашырау сызбасы (корреляциялық диаграмма, корреляциялық өріс, шашырау диаграммасы) – нүктелер қосылмаған кездегі нүктелердің графигі. Екі айнымалы үшін деректерді көрсету үшін пайдаланылады, олардың бірі фактор, екіншісі нәтиже. Оның көмегімен деректер жұптарының графикалық көрінісі координаталық жазықтықта нүктелер жиыны («бұлттар») түрінде жүзеге асырылады;
- Бағаналы диаграмма – тік бағандар түріндегі график;
- сектор немесе дөңгелек диаграмма (Дөңгелек диаграмма). Мұндай диаграмма әрқайсысының ауданы өз бөлігіне пропорционал болатын бірнеше сегменттерге-секторларға бөлінеді;
- жәшік сызбасы (мұртшасы бар қорап, мұртшасы бар қорап, Қораптың сызбасы, қорап-мұрт диаграммасы). Бұл статистикалық деректерді көрсету үшін ең жиі қолданылатын нұсқа. Бұл диаграммадағы ақпарат өте мазмұнды және пайдалы. Ол вариациялық қатарды сипаттайтын бірнеше мәндерді бір уақытта көрсетеді: ең төменгі және максималды мәндер, орташа және медиана, бірінші және үшінші квартилдер.
- Матрицаны оқуға немесе құруға арналған құралдар. Палитра құралдарын пайдалану үшін сізде матрица түріндегі бастапқы деректер болуы керек - бір өлшемді массив. Оны құжатта ағымдағы сеанспен жасауға және одан кейін оның атауын жалпы математика панелін пайдаланып теңдеулерді шешу сияқты палитра құралдарының терезелерінде енгізу ретінде ауыстыруға болады. Сондай-ақ деректерді енгізу деректерін енгізу терезелеріне деректерді тікелей енгізуге болады. Бұл жағдайда олар жүйеде қабылданған пішінде, яғни төртбұрышты жақшаға енгізіледі және үтір арқылы бөлінеді. Бірінші нұсқа әлдеқайда жақсы екені анық, өйткені ол тек бір реттік деректерді енгізуді қажет етеді.
Панельден басқа, барлық статистикалық құралдарды сәйкес функциялар арқылы да пайдалануға болады.
Максима- символдық және сандық өрнектермен жұмыс істеуге мүмкіндік беретін компьютерлік жүйе. Серияларды кеңейту, дифференциалдау, Лаплас түрлендіру, интеграция операцияларын қолдайды. Бағдарлама қарапайым дифференциалдық теңдеулер, матрицалар мен тензорлар, сызықтық теңдеулер жүйелері, тізімдер, векторлар, көпмүшелер, жиындардан қорықпайды. Компьютерлік есептеу жүйесі жоғары дәлдікпен есептеулер жасай алады. Бүтін және бөлшек өрнектерді қолданады. Қолданба екі немесе үш өлшемді графиктерді құра алады. Онда утилитамен қалай жұмыс істеу керектігі, қандай операторларға математикалық амалдар жүйесі қолдау көрсететіні егжей-тегжейлі сипатталған нұсқаулық бар. Бағдарлама компьютерлік алгебра әуесқойлары үшін өте қолайлы: студенттер, мұғалімдер, аспиранттар.


- Математикалық сандық және символдық өрнектермен жұмыс жасайды.
- Тізімдермен, көпмүшеліктермен, матрицалармен, тензорлармен, дифференциалдық теңдеулермен және сызықтық теңдеулер жүйесімен жұмыс істеуді қолдайды.
- серияларды кеңейту, дифференциалдау, Лаплас түрлендіру, интеграция операцияларын қолдайды.
- Есептерді жоғары дәлдікпен орындайды.
- Натурал сандарды, бөлшек өрнектерді қолданады.
- Екі өлшемді немесе үш өлшемді өлшемдерде графиктерді құрастыра алады.
- Компьютерлік алгебра әуесқойлары үшін қолайлы.
- Жүйенің жұмысымен танысу үшін қолжетімді құжаттама бар.
- Жұмыс ортасының өнімділігі мен жылдамдығына әсер етпейді.
– Орыс тілін қолдау бар.
Бағдарламаның кемшіліктері
- Портативті нұсқасы жоқ.- 1200 МГц немесе одан да қуатты тактілік жиілігі бар процессор.
- ЖЖҚ 256 МБ немесе одан көп.
- 185 Мбайттан бастап қатты дискідегі бос орын.
- 32 биттік немесе 64 биттік архитектура (x86 немесе x64).
- Операциялық жүйе Windows XP, Windows Vista, Windows 7, Windows 8
Көп функциялы калькуляторлар: салыстыру кестелері
| Бағдарламаның аты | Орыс тілінде | Бөлулер | Орнатушы | Танымалдық | Өлшем | Индекс |
| ★ ★ ★ ★ ★ | 48,7 Мб | 100 | ||||
| ★ ★ ★ ★ ★ | 59,8 Мб | 99 | ||||
| ★ ★ ★ ★ ★ | 1,3 МБ | 86 | ||||
Maxima жүйесінде көптеген кіріктірілген функциялар бар. Әрбір кірістірілген функцияны анықтамалық жүйедегі құжаттамада сипаттауға болады. Анықтамаға F1 функционалдық пернесі арқылы қол жеткізуге болады. Maxima сонымен қатар нақты сөздер үшін құжаттамадан ақпарат беретін арнайы функцияға ие. Бұл функция шақыруының қысқартылған нұсқасы: ?? атауы (Cурет 12). Мұнда?? оператордың аты болып табылады және аргумент одан бос орынмен бөлінуі керек. Оператор?? көрсетілген мәтінді қамтитын анықтама бөлімдерінің және функция атауларының тізімін көрсетеді, содан кейін олар сізге қарағыңыз келетін бөлімнің нөмірін немесе функцияның сипаттамасын енгізуді ұсынады:
12-сурет. Қызықтыратын Maxima жүйесінің пәрмені бойынша анықтамаға қоңырау шалу
Maxima жүйесінде операторлар мен функциялар арасында нақты айырмашылық жоқ екенін ескеріңіз. Оның үстіне, әрбір мәлімдеме шын мәнінде функция болып табылады.
Барлық Maxima функциялары мен операторлары тек нақты сандармен ғана емес, күрделі сандармен де жұмыс істейді. Күрделі сандардың өзі алгебралық түрде жазылады, елестету бірлігі %i арқылы белгіленеді; яғни a+b*%i түрінде, мұндағы АЖәне б- сәйкесінше санның нақты және жорамал бөліктері.
қарастырайық негізгі функция синтаксисіМаксималды жүйелер.
1. Арифметикалық операторлар: + , -, *, /, -->. Мысалы:

3. Логикалық операторлар: және, немесе, емес. Мысалы:

4. Санның факториалын табу функциясы: !
Факториал ең жалпы түрде берілген және шын мәнінде гамма-функция (дәлірек айтқанда, x! = гамма(x+1)), яғни теріс бүтін сандардан басқа барлық күрделі сандар жиынында анықталады. Натурал санның (және нөлдің) факториалы бірдей натурал санға автоматты түрде жеңілдетіледі.
![]()
5. Жартылай факторды табу функциясы: !! (барлық жұп (жұп операнд үшін) немесе берілгеннен кіші немесе оған тең тақ сандардың көбейтіндісі).
6. Синтаксистік теңдік терістеу қызметі: # a#b белгісі a=b емес мәніне тең. 
7. x санының модулін табу функциясы: abs(x) Модуль барлық комплекс сандар үшін анықталған. Мысалы:

8. x санының таңбасын қайтаратын функция: signum(x)

9. Берілген нақты сандардың ең үлкен және ең кіші мәндерін қайтаратын функциялар: max(x1,...,xn) және min(x1,...,xn).

10. Кейбір кірістірілген математикалық функциялар:
| sqrt(x) | х-тің квадрат түбірі |
| acos(x) | Аргументтің арккозинусы x |
| acosh (x) | х-тің гиперболалық арккозинусы |
| acot(x) | x аргументінің аркотангенсі |
| acoth (x) | х аргументінің гиперболалық арккотангенсі |
| acsc(x) | x аргументінің арккосеканты |
| acsch(x) | x аргументінің гиперболалық аркокосеканты |
| asec(x) | x аргументінің доғасы |
| asech(x) | x аргументінің гиперболалық доғасы |
| asin(x) | Аргументтің арксинусы x |
| асинх(x) | x аргументінің гиперболалық доғасы |
| атан(x) | x аргументінің арктангенсі |
| атанх (x) | х аргументінің гиперболалық артангенсі |
| cosh(x) | х аргументінің гиперболалық косинусы |
| coth(x) | х аргументінің гиперболалық котангенсі |
| csc(x) | x аргументінің косеканты |
| csch(x) | x аргументінің гиперболалық косеканты |
| сек(x) | Аргументтің бөлінісі x |
| sech(x) | x аргументінің гиперболалық секантасы |
| күнә(x) | х синусы |
| sinh(x) | х-тің гиперболалық синусы |
| күңгірт(x) | Тангенс x |
| тан(x) | х аргументінің гиперболалық тангенсі |
| журнал(x) | х-тің натурал логарифмі |
| Exp(x) | Көрсеткіш x |
11. Матрицалармен жұмыс істеу функциялары:
анықтауыш – матрицаның анықтауышын табу:
меншікті мәндер – матрицаның меншікті мәндерін табу:
төңкеру– кері матрицаны алу:

кәмелетке толмаған– матрицаның минорын анықтайды. Бірінші аргумент матрица, екіншісі және
үшінші – тиісінше жол және баған индекстері:
дәреже– матрицалық дәреже:
субматрица– жою арқылы түпнұсқадан алынған матрицаны қайтарады
сәйкес жолдар және (немесе) бағандар. Параметрлері:
жойылатын жолдар саны, бастапқы матрица, жойылатын бағандар саны.

ауыстыру– матрицалық транспозиция:

Maxima жүйелік тілінде кез келген бағдарламалау тілінде кездесетін негізгі орындалатын операторлар бар. Оларды қарастырайық.
Мәндерді тағайындау операторлары (өрнектерді атау).
1. «:» операторы (айнымалының мәнін орнату операторы).
2. «:=» операторы (пайдаланушы функциясын көрсетуге арналған оператор).
3.Тағайындау және функция тағайындау операторларының кеңейтілген нұсқалары, сәйкесінше:: және::= арқылы белгіленеді.
Пайдаланушы функциясының операторын пайдалану пайдаланушы функциясымен жұмыс істеуді әлдеқайда жеңілдетеді, себебі оған аты бойынша қол жеткізуге болады және берілген нүктелердегі функция мәндерін оңай және ыңғайлы есептеуге болады.
Мысалы: функцияның мәнін табыңыз f (x,y)=cosx + sin жнүктесінде

Цикл операторы.Цикл операторын бірнеше жолмен көрсетуге болады. Нақтылау әдісі цикл денесін қанша рет орындау қажет екендігі алдын ала белгілі болғанына байланысты.
Мысал: айнымалы мәндерді көрсету үшін циклды орнату А-3-тен 10-ға дейінгі аралықта 5 қадаммен:

Maxima жүйесінің келесі маңызды ерекшелігі болып табылады тізімдермен және массивтермен жұмыс.
Тізімдерді жасау үшін makelist пәрменін пайдаланыңыз. Мысалы, пәрменді пайдалану

біз мәндері формула бойынша табылған он элементтен тұратын x деп аталатын тізім құрдық.
Массивтерді қалыптастыру үшін массив командасын пайдаланыңыз. Мысалы, пәрменді пайдаланып,
![]()
біз 10 жол мен 5 бағаннан тұратын екі өлшемді А массивін құрдық. Массивті элементтермен толтыру үшін параметрі бар циклды қолданамыз. Мысалы,
Жиым элементтерін экранда көрсету үшін мына пәрменді қолдануға болады:
Массив алдын ала декларациясыз құрылуы мүмкін. Келесі мысалда біз 5 элементтен тұратын бір өлшемді x массивін құрдық, оның мәндері x формуласы арқылы есептеледі мен)=күнә мен

Массивтермен жұмыс істеудің ыңғайсыздығы массив элементтерінің мәндері бағанда көрсетіледі. Егер (екі өлшемді) массивтің мәндері матрица ретінде көрсетілсе, бұл әлдеқайда ыңғайлы. Осы мақсаттар үшін genmatrix командасын пайдалануға болады. Мысалы, екі өлшемді массив (матрица) жасау үшін келесі пішінде пәрменді көрсету керек:
Алынған массивді шығарайық:

6. Өрнектің ең қарапайым түрлендірулері.
Әдепкі бойынша, Autosimplification функциясы Maxima жүйесінде белсенді, яғни. жүйе енгізілген өрнектің өзін ешбір пәрменсіз жеңілдетуге тырысады.
Мысал. Келесі сандық өрнектің мәнін табу керек делік:
Өрнекті Maxima жүйе тілінің ережелері бойынша орнатайық.

Көріп отырғаныңыздай, біз ешқандай пәрменді көрсетпесек те, жүйе өрнектің мәнімен жауап берді.
Жүйені нәтижені емес, өрнектің өзін шығаруға қалай мәжбүрлеуге болады? Ол үшін simp: false$ пәрмені арқылы оңайлату функциясын өшіру керек. Сонда біз аламыз:

Жеңілдету функциясын белсендіру үшін simp:true$ пәрменін көрсету керек. Автоматты жеңілдету функциясы сандық және кейбір сандық емес өрнектермен де жұмыс істей алады. Мысалы,

Енгізу кезінде біз алдыңғы ұяшықтардың кез келгеніне оның атымен сілтеме жасай аламыз, оны кез келген өрнекте ауыстырамыз. Сонымен қатар, соңғы шығыс ұяшығы %, ал соңғы кіріс ұяшығы _ арқылы белгіленеді. Бұл соңғы нәтижеге оның санына алаңдамай сілтеме жасауға мүмкіндік береді. Бірақ ұяшықтарға мұндай қоңырауларды теріс пайдаланбау керек, өйткені бүкіл құжатты немесе оның жеке кіріс ұяшықтарын қайта қарау кезінде ұяшық нөмірлері арасында сәйкессіздік орын алуы мүмкін.
Мысал. Өрнектің мәнін тауып, нәтижені 5 есе көбейтіңіз.

Ұяшық атауларының орнына айнымалыларды қолданып, олардың атауларын кез келген өрнектерге тағайындаған жөн. Бұл жағдайда кез келген математикалық өрнек айнымалының мәні ретінде әрекет ете алады.
Айнымалы атауларының мәндері құжатпен бүкіл жұмыс барысында сақталады. Еске салайық, егер айнымалыдан анықтаманы алып тастау қажет болса, мұны kill(name) функциясы арқылы жасауға болады, мұндағы name - жойылатын өрнектің аты; сонымен қатар, бұл сіз тағайындаған атау немесе кез келген кіріс немесе шығыс ұяшығы болуы мүмкін. Сол сияқты, kill(all) пәрменін енгізу (немесе мәзірді таңдау) арқылы барлық жадты өшіруге және барлық атауларды босатуға болады. Мақта->Таза жад(Жадты тазалау)). Бұл жағдайда барлық енгізу/шығару ұяшықтары да тазартылады және олардың нөмірленуі қайтадан бірден басталады.
Автоматты жеңілдету функциясы әрқашан өрнекті жеңілдете алмайды. Оған қоса, өрнектермен жұмыс істеуге арналған бірқатар командалар бар: ұтымды және иррационал. Олардың кейбіреулерін қарастырайық.
егеуқұйрық (өрнек) - рационал өрнекті канондық түрге түрлендіреді: барлық жақшаларды ашады, содан кейін барлығын ортақ бөлгішке келтіреді, қосады және азайтады; ақырлы ондық жүйедегі барлық сандарды рационал сандарға түрлендіреді. Кез келген ұтымды емес түрлендірулер кезінде канондық пішін автоматты түрде «жойылады».
ratsimp (өрнек) - рационал түрлендірулер арқылы өрнекті жеңілдетеді. Ол сондай-ақ «терең» жұмыс істейді, яғни өрнектің иррационалды бөліктері атомдық болып саналмайды, бірақ олардың ішіндегі барлық ұтымды элементтерді қоса алғанда, жеңілдетілген.
fullratsimp(өрнек) – берілген өрнекке ratsimp() функциясын ретімен қолдану арқылы рационал өрнекті жеңілдетуге арналған функция. Осыған байланысты функция ratsimp() функциясына қарағанда біршама баяу, бірақ сенімдірек нәтиже береді.
кеңейту (өрнек) - барлық ұя салу деңгейлеріндегі өрнектегі жақшаларды кеңейтеді. ratexpand() функциясынан айырмашылығы, ол бөлшектерді ортақ бөлгішке келтірмейді.
radcan(өрнек) - логарифмдік, көрсеткіштік және дәрежелік функцияларды бүтін емес рационал көрсеткішті көрсеткіштермен, яғни түбірлерімен (радикалдары) оңайлатуға арналған функция.
Көбінесе Максимадағы өрнекті жеңілдетуге тырысқанда, ол шын мәнінде оны тек күрделірек етеді. Нәтиженің артуы өрнекке енгізілген айнымалылар қандай мәндерді қабылдай алатыны белгісіз болғандықтан орын алуы мүмкін. Бұған жол бермеу үшін айнымалы қабылдай алатын мәндерге шектеулер қою керек. Бұл assume (шарт) функциясы арқылы орындалады. Сондықтан кейбір жағдайларда radcan() мен ratsimp() немесе fullratsimp() біріктіру арқылы ең жақсы нәтижеге қол жеткізуге болады.