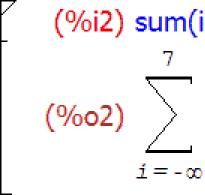Περιγραφή Maxima. Πώς να δουλέψετε με τα maxima
Το πακέτο μαθηματικών Maxima είναι μια από τις καλύτερες δωρεάν αντικαταστάσεις για το MathCAD.
Αυτό το εγχειρίδιο (σε μορφή pdf) μπορεί να χρησιμοποιηθεί στους κλάδους της μαθηματικής ανάλυσης, των διαφορικών εξισώσεων, των πακέτων λογισμικού εφαρμογών κ.λπ. σε διάφορες ειδικότητες σε ιδρύματα τριτοβάθμιας επαγγελματικής εκπαίδευσης, εάν το κρατικό εκπαιδευτικό πρότυπο προβλέπει τη μελέτη της ενότητας «Διαφορικό Εξισώσεις», καθώς και σε μαθήματα επιλογής. Μπορεί επίσης να είναι χρήσιμο για εξοικείωση με συστήματα μαθηματικών υπολογιστών σε εξειδικευμένες τάξεις ιδρυμάτων γενικής εκπαίδευσης με εις βάθος μελέτη των μαθηματικών και της επιστήμης των υπολογιστών.
- Πρόλογος
- Κεφάλαιο 1. Βασικές αρχές εργασίας στο σύστημα μαθηματικών υπολογιστών Maxima
- 1.1. Σχετικά με το σύστημα Maxima
- 1.2. Εγκατάσταση του Maxima σε προσωπικό υπολογιστή
- 1.3. Διεπαφή κύριου παραθύρου Maxima
- 1.4. Εργασία με κελιά στο Maxima
- 1.5. Εργασία με το σύστημα βοήθειας Maxima
- 1.6. Λειτουργίες και εντολές του συστήματος Maxima
- 1.7. Διαχείριση της διαδικασίας υπολογισμού στο Maxima
- 1.8. Απλοί μετασχηματισμοί έκφρασης
- 1.9. Επίλυση αλγεβρικών εξισώσεων και των συστημάτων τους
- 1.10. Δυνατότητες γραφικών
- Κεφάλαιο 2. Αριθμητικές μέθοδοι επίλυσης διαφορικών εξισώσεων
- 2.1. Γενικές πληροφορίες για τις διαφορικές εξισώσεις
- 2.2. Αριθμητικές μέθοδοι επίλυσης του προβλήματος Cauchy για μια συνηθισμένη διαφορική εξίσωση πρώτης τάξης
- 2.2.1. Μέθοδος Euler
- 2.2.2. Μέθοδος Euler-Cauchy
- 2.2.3. Μέθοδος Runge-Kutta 4 τάξεις ακρίβειας
- 2.3. Επίλυση προβλημάτων συνοριακών τιμών για συνηθισμένες διαφορικές εξισώσεις χρησιμοποιώντας τη μέθοδο των πεπερασμένων διαφορών
- 2.4. Μέθοδος πλέγματος για την επίλυση μερικών διαφορικών εξισώσεων
- Κεφάλαιο 3. Εύρεση λύσεων διαφορικών εξισώσεων στο σύστημα Maxima
- 3.1. Ενσωματωμένες συναρτήσεις για την εύρεση λύσεων σε διαφορικές εξισώσεις
- 3.2. Επίλυση διαφορικών εξισώσεων και των συστημάτων τους σε συμβολική μορφή
- 3.3. Κατασκευή τροχιών και πεδίων κατεύθυνσης διαφορικών εξισώσεων.
- 3.4. Εφαρμογή αριθμητικών μεθόδων για την επίλυση του προβλήματος Cauchy για συνηθισμένες διαφορικές εξισώσεις
- 3.4.1. Μέθοδος Euler
- 3.4.2. Μέθοδος Euler-Cauchy
- 3.4.3. Μέθοδος Runge-Kutta
- 3.5. Εφαρμογή μιας μεθόδου πεπερασμένων διαφορών για την επίλυση ενός προβλήματος οριακών τιμών για συνηθισμένες διαφορικές εξισώσεις
- 3.6. Εφαρμογή της μεθόδου πλέγματος για μερικές διαφορικές εξισώσεις
- Εργασίες για ανεξάρτητη λύση
- Βιβλιογραφία
Πρόλογος
Η θεωρία των διαφορικών εξισώσεων είναι ένας από τους μεγαλύτερους κλάδους των σύγχρονων μαθηματικών. Ένα από τα κύρια χαρακτηριστικά των διαφορικών εξισώσεων είναι η άμεση σύνδεση μεταξύ της θεωρίας των διαφορικών εξισώσεων και των εφαρμογών. Όταν μελετά οποιοδήποτε φυσικό φαινόμενο, ο ερευνητής, πρώτα απ 'όλα, δημιουργεί τη μαθηματική εξιδανίκευση ή το μαθηματικό του μοντέλο, καταγράφει τους βασικούς νόμους που διέπουν αυτό το φαινόμενο σε μαθηματική μορφή. Πολύ συχνά αυτοί οι νόμοι μπορούν να εκφραστούν με τη μορφή διαφορικών εξισώσεων. Αποδεικνύεται ότι πρόκειται για μοντέλα διαφόρων φαινομένων μηχανικής συνεχούς, χημικών αντιδράσεων, ηλεκτρικών και μαγνητικών φαινομένων κ.λπ. Μελετώντας τις προκύπτουσες διαφορικές εξισώσεις μαζί με πρόσθετες συνθήκες, οι οποίες, κατά κανόνα, καθορίζονται με τη μορφή αρχικών και οριακών συνθηκών , ο μαθηματικός λαμβάνει πληροφορίες για το φαινόμενο που εμφανίζεται, μερικές φορές μπορεί να ανακαλύψει το παρελθόν και το μέλλον του.
Για να συντάξετε ένα μαθηματικό μοντέλο με τη μορφή διαφορικών εξισώσεων, κατά κανόνα, πρέπει να γνωρίζετε μόνο τοπικές συνδέσεις και να μην χρειάζεστε πληροφορίες για ολόκληρο το φυσικό φαινόμενο ως σύνολο. Ένα μαθηματικό μοντέλο καθιστά δυνατή τη μελέτη ενός φαινομένου στο σύνολό του, την πρόβλεψη της εξέλιξής του και την πραγματοποίηση ποιοτικών αξιολογήσεων των μετρήσεων που συμβαίνουν σε αυτό με την πάροδο του χρόνου. Τα ηλεκτρομαγνητικά κύματα ανακαλύφθηκαν με βάση την ανάλυση διαφορικών εξισώσεων.
Μπορούμε να πούμε ότι η ανάγκη επίλυσης διαφορικών εξισώσεων για τις ανάγκες της μηχανικής, δηλαδή να βρεθούν τροχιές κίνησης, ήταν με τη σειρά της η ώθηση για τον Νεύτωνα να δημιουργήσει έναν νέο λογισμό. Οι εφαρμογές του νέου λογισμού σε προβλήματα γεωμετρίας και μηχανικής έγιναν μέσω συνηθισμένων διαφορικών εξισώσεων.
Λαμβάνοντας υπόψη τη σύγχρονη ανάπτυξη της τεχνολογίας των υπολογιστών και την εντατική ανάπτυξη μιας νέας κατεύθυνσης - τα μαθηματικά υπολογιστών - τα πακέτα λογισμικού που ονομάζονται συστήματα μαθηματικών υπολογιστών έχουν γίνει ευρέως διαδεδομένα και σε ζήτηση.
Τα μαθηματικά υπολογιστών είναι μια νέα κατεύθυνση στην επιστήμη και την εκπαίδευση που προέκυψε στη διασταύρωση των θεμελιωδών μαθηματικών, της πληροφορίας και των τεχνολογιών υπολογιστών. Ένα σύστημα μαθηματικών υπολογιστών (SCM) είναι ένα σύνολο προγραμμάτων που παρέχει αυτοματοποιημένη, τεχνολογικά ενοποιημένη και κλειστού βρόχου επεξεργασία μαθηματικών προβλημάτων κατά τον καθορισμό συνθηκών σε μια ειδικά σχεδιασμένη γλώσσα.
Τα σύγχρονα μαθηματικά συστήματα ηλεκτρονικών υπολογιστών είναι προγράμματα με γραφική διεπαφή πολλαπλών παραθύρων και ανεπτυγμένο σύστημα βοήθειας, που τα καθιστά ευκολότερα στην εκμάθηση και τη χρήση τους. Οι κύριες τάσεις στην ανάπτυξη του SCM είναι η ανάπτυξη των μαθηματικών δυνατοτήτων, ειδικά στον τομέα των αναλυτικών και συμβολικών υπολογισμών, η σημαντική επέκταση των εργαλείων οπτικοποίησης για όλα τα στάδια των υπολογισμών, η ευρεία χρήση 2D και 3D γραφικών, η ενσωμάτωση διαφόρων συστήματα μεταξύ τους και άλλο λογισμικό, ευρεία πρόσβαση στο Διαδίκτυο, οργάνωση συνεργασίας σε εκπαιδευτικά και επιστημονικά έργα στο Διαδίκτυο, χρήση εργαλείων κινούμενων εικόνων και επεξεργασίας εικόνας, εργαλείων πολυμέσων κ.λπ.
Μια σημαντική περίσταση που μέχρι πρόσφατα εμπόδιζε την ευρεία χρήση του SCM στην εκπαίδευση είναι το υψηλό κόστος του επαγγελματικού επιστημονικού μαθηματικού λογισμικού. Ωστόσο, πρόσφατα, πολλές εταιρείες που αναπτύσσουν και διανέμουν τέτοια προγράμματα παρουσιάζουν (μέσω Διαδικτύου - http://www.softline.ru) προηγούμενες εκδόσεις των προγραμμάτων τους για δωρεάν χρήση, χρησιμοποιούν ευρέως ένα σύστημα εκπτώσεων για εκπαιδευτικά ιδρύματα και διανέμουν επίδειξη ή δοκιμαστικές εκδόσεις για δωρεάν προγράμματα
Επιπλέον, εμφανίζονται δωρεάν ανάλογα συστήματα μαθηματικών υπολογιστών, για παράδειγμα, Maxima, Scilab, Octave κ.λπ.
Αυτό το σεμινάριο εξετάζει τις δυνατότητες του συστήματος μαθηματικών υπολογιστών Maxima για την εύρεση λύσεων σε διαφορικές εξισώσεις.
Γιατί Maxima;
Πρώτον, το σύστημα Maxima είναι ένα μη κερδοσκοπικό έργο ανοιχτού κώδικα. Το Maxima ανήκει σε μια κατηγορία προϊόντων λογισμικού που διανέμονται υπό την GNU GPL (General Public License).Δεύτερον, το Maxima είναι ένα πρόγραμμα για την επίλυση μαθηματικών προβλημάτων τόσο σε αριθμητική όσο και σε συμβολική μορφή. Το φάσμα των δυνατοτήτων του είναι πολύ ευρύ: ενέργειες για μετασχηματισμό παραστάσεων, εργασία με μέρη παραστάσεων, επίλυση προβλημάτων γραμμικής άλγεβρας, μαθηματική ανάλυση, συνδυαστική, θεωρία αριθμών, ανάλυση τανυστών, στατιστικά προβλήματα, κατασκευή γραφημάτων συναρτήσεων στο επίπεδο και στο διάστημα σε διάφορα συστήματα συντεταγμένων κ.λπ. δ.
Τρίτον, το Maxima διαθέτει πλέον ένα ισχυρό, αποτελεσματικό και φιλικό προς το χρήστη γραφικό περιβάλλον εργασίας μεταξύ πλατφορμών που ονομάζεται WxMaxima (http://wxmaxima.sourceforge.net).
Οι συγγραφείς του βιβλίου μελετούν συστήματα μαθηματικών υπολογιστών όπως Mathematica, Maple, MathCad εδώ και δέκα χρόνια. Ως εκ τούτου, γνωρίζοντας τις δυνατότητες αυτών των προϊόντων λογισμικού, ιδιαίτερα για την εύρεση λύσεων σε διαφορικές εξισώσεις, ήθελα να μελετήσω το θέμα που σχετίζεται με την οργάνωση των υπολογισμών σε συμβολική μορφή σε ελεύθερα κατανεμημένα συστήματα μαθηματικών υπολογιστών.
Αυτό το εγχειρίδιο μιλά για τις δυνατότητες οργάνωσης της διαδικασίας αναζήτησης λύσεων σε διαφορικές εξισώσεις με βάση το σύστημα Maxima και περιέχει γενικές πληροφορίες για την οργάνωση της εργασίας στο σύστημα.
Το εγχειρίδιο αποτελείται από 3 κεφάλαια. Το πρώτο κεφάλαιο εισάγει τους αναγνώστες στη γραφική διεπαφή wxMaxima του συστήματος Maxima, τις δυνατότητες εργασίας σε αυτό και τη σύνταξη της γλώσσας συστήματος. Η εξέταση του συστήματος ξεκινά με το πού μπορείτε να βρείτε τη διανομή του συστήματος και πώς να το εγκαταστήσετε. Στο δεύτερο κεφάλαιο συζητούνται γενικά θέματα της θεωρίας των διαφορικών εξισώσεων και αριθμητικές μέθοδοι επίλυσής τους.
Το τρίτο κεφάλαιο είναι αφιερωμένο στις ενσωματωμένες συναρτήσεις του συστήματος μαθηματικών υπολογιστών Maxima για την εύρεση λύσεων σε συνηθισμένες διαφορικές εξισώσεις 1ης και 2ης τάξης σε συμβολική μορφή. Επίσης στο τρίτο κεφάλαιο παρουσιάζεται η εφαρμογή αριθμητικών μεθόδων επίλυσης διαφορικών εξισώσεων στο σύστημα Maxima. Στο τέλος του εγχειριδίου υπάρχουν εργασίες για ανεξάρτητη λύση.
Ελπίζουμε ότι ένα ευρύ φάσμα χρηστών θα ενδιαφερθεί για το εγχειρίδιο και ότι θα γίνει ο βοηθός τους στην εκμάθηση ενός νέου εργαλείου για την επίλυση μαθηματικών προβλημάτων.
Τ.Ν. Gubina, E.V. Αντρόποβα
Yelets, Ιούλιος 2009
ΥΣΤΕΡΟΓΡΑΦΟ. Γρήγορη εκκίνηση: για την εκτέλεση εντολώνκαι λειτουργεί στο mwMaxima, πρέπει πρώτα να εισάγετε την ίδια την εντολή και μετά να πατήσετε crtl+Enter.
Πράξεις μαθηματικής ανάλυσης
Ποσά
Η συνάρτηση αθροίσματος χρησιμοποιείται για την εύρεση ποσών. Σύνταξη συνάρτησης:
Άθροισμα (έκφραση, μεταβλητή, κατώτερο όριο μεταβολής μεταβλητής, ανώτερο όριο μεταβολής μεταβλητής)
Για παράδειγμα:
Εάν αντιστοιχίσετε την τιμή της μεταβλητής συστήματος θετικό άπειρο "inf" στο τελευταίο όρισμα, αυτό θα υποδηλώνει την απουσία ενός άνω ορίου και θα υπολογιστεί ένα άπειρο άθροισμα. Επίσης, ένα άπειρο άθροισμα θα υπολογιστεί εάν αντιστοιχίσετε την τιμή της μεταβλητής αρνητικού συστήματος απείρου "minf" στο όρισμα "κατώτερο όριο μεταβολής μεταβλητής". Οι ίδιες τιμές χρησιμοποιούνται και σε άλλες συναρτήσεις μαθηματικής ανάλυσης.
Για παράδειγμα:

Εργα
Για να βρείτε πεπερασμένα και άπειρα γινόμενα, χρησιμοποιήστε τη συνάρτηση προϊόντος. Έχει τα ίδια ορίσματα με τη συνάρτηση αθροίσματος.
Για παράδειγμα:

Όρια
Για να βρείτε όρια, χρησιμοποιήστε τη συνάρτηση ορίου.
Σύνταξη συνάρτησης:
όριο (έκφραση, μεταβλητή, σημείο διακοπής)
Εάν το όρισμα "σημείο διακοπής" οριστεί σε "inf", τότε αυτό θα υποδηλώνει την απουσία περιγράμματος.
Για παράδειγμα:

Για τον υπολογισμό των μονόπλευρων ορίων, χρησιμοποιείται ένα πρόσθετο όρισμα, το οποίο έχει την τιμή συν για τον υπολογισμό των ορίων στα δεξιά και μείον για τα αριστερά.
Για παράδειγμα, ας μελετήσουμε τη συνέχεια της συνάρτησης arctan(1/(x - 4)). Αυτή η συνάρτηση είναι απροσδιόριστη στο σημείο x = 4. Ας υπολογίσουμε τα όρια δεξιά και αριστερά:

Όπως μπορούμε να δούμε, το σημείο x = 4 είναι ένα σημείο ασυνέχειας πρώτου είδους για αυτή τη συνάρτηση, αφού υπάρχουν όρια στα αριστερά και στα δεξιά, τα οποία είναι ίσα με -PI/2 και PI/2, αντίστοιχα.
Διαφορικά
Η συνάρτηση diff χρησιμοποιείται για την εύρεση διαφορών. Σύνταξη συνάρτησης:
diff(έκφραση, μεταβλητή1, σειρά παραγώγου για τη μεταβλητή1 [,μεταβλητή2, σειρά παραγώγου για τη μεταβλητή2,...])
όπου η έκφραση είναι η συνάρτηση που διαφοροποιείται, το δεύτερο όρισμα είναι η μεταβλητή ως προς την οποία πρέπει να ληφθεί η παράγωγος, το τρίτο (προαιρετικό) είναι η σειρά της παραγώγου (από προεπιλογή - η πρώτη τάξη).
Για παράδειγμα:

Γενικά, μόνο το πρώτο όρισμα απαιτείται για τη συνάρτηση diff. Σε αυτήν την περίπτωση, η συνάρτηση επιστρέφει το διαφορικό της έκφρασης. Το διαφορικό της αντίστοιχης μεταβλητής συμβολίζεται με del(όνομα μεταβλητής):

Όπως μπορούμε να δούμε από τη σύνταξη της συνάρτησης, ο χρήστης έχει την ευκαιρία να ορίσει ταυτόχρονα πολλές μεταβλητές διαφοροποίησης και να ορίσει τη σειρά για καθεμία από αυτές:

Εάν χρησιμοποιείτε μια παραμετρική συνάρτηση, η μορφή γραφής της συνάρτησης αλλάζει: μετά το όνομα της συνάρτησης γράφονται τα σύμβολα ":=" και η πρόσβαση στη συνάρτηση γίνεται μέσω του ονόματός της με μια παράμετρο:

Η παράγωγος μπορεί να υπολογιστεί σε ένα δεδομένο σημείο. Αυτό γίνεται ως εξής:

Η συνάρτηση diff χρησιμοποιείται επίσης για τον προσδιορισμό παραγώγων σε διαφορικές εξισώσεις, όπως συζητείται παρακάτω.
Ολοκληρώματα
Για να βρείτε ολοκληρώματα στο σύστημα, χρησιμοποιήστε τη συνάρτηση ενσωμάτωσης. Για να βρεθεί το αόριστο ολοκλήρωμα μιας συνάρτησης, χρησιμοποιούνται δύο ορίσματα: το όνομα της συνάρτησης και η μεταβλητή στην οποία πραγματοποιείται η ολοκλήρωση. Για παράδειγμα:

Εάν η απάντηση είναι διφορούμενη, το Maxima μπορεί να κάνει μια επιπλέον ερώτηση:
Η απάντηση πρέπει να περιέχει το κείμενο από την ερώτηση. Σε αυτήν την περίπτωση, εάν η τιμή της μεταβλητής y είναι μεγαλύτερη από "0", θα είναι "θετική", και διαφορετικά - "αρνητική". Σε αυτήν την περίπτωση, μόνο το πρώτο γράμμα της λέξης μπορεί να εισαχθεί.
Για να βρείτε ένα συγκεκριμένο ολοκλήρωμα σε μια συνάρτηση, πρέπει να καθορίσετε πρόσθετα ορίσματα: όρια του ολοκληρώματος:
Το Maxima επιτρέπει επίσης άπειρα όρια ολοκλήρωσης. Για να γίνει αυτό, οι τιμές "-inf" και "inf" χρησιμοποιούνται για το τρίτο και τέταρτο ορίσματα της συνάρτησης:

Για να βρείτε την κατά προσέγγιση τιμή του ολοκληρώματος σε αριθμητική μορφή, όπως σημειώθηκε νωρίτερα, θα πρέπει να επιλέξετε το αποτέλεσμα στο κελί εξόδου, να καλέσετε το μενού περιβάλλοντος σε αυτό και να επιλέξετε το στοιχείο "To Float" από αυτό (μετατροπή σε αριθμό κινητής υποδιαστολής) .

Το σύστημα είναι επίσης ικανό να υπολογίζει πολλαπλά ολοκληρώματα. Για να γίνει αυτό, οι συναρτήσεις ολοκλήρωσης είναι ένθετες η μία μέσα στην άλλη. Ακολουθούν παραδείγματα υπολογισμού διπλού αόριστου και διπλού ορισμένου ολοκληρώματος:

Λύσεις διαφορικών εξισώσεων
Όσον αφορά τις δυνατότητές του στην επίλυση διαφορικών εξισώσεων, το Maxima είναι αισθητά κατώτερο από, για παράδειγμα, το Maple. Αλλά το Maxima εξακολουθεί να σας επιτρέπει να επιλύετε συνηθισμένες διαφορικές εξισώσεις πρώτης και δεύτερης τάξης, καθώς και τα συστήματά τους. Για να γίνει αυτό, ανάλογα με το σκοπό, χρησιμοποιούνται δύο λειτουργίες. Για τη γενική λύση συνηθισμένων διαφορικών εξισώσεων, χρησιμοποιείται η συνάρτηση ode2 και για την εύρεση λύσεων σε εξισώσεις ή συστήματα εξισώσεων με βάση αρχικές συνθήκες, χρησιμοποιείται η συνάρτηση desolve.
Η συνάρτηση ode2 έχει την ακόλουθη σύνταξη:
ode2(εξίσωση, εξαρτημένη μεταβλητή, ανεξάρτητη μεταβλητή);
Η συνάρτηση diff χρησιμοποιείται για την ένδειξη παραγώγων σε διαφορικές εξισώσεις. Αλλά σε αυτή την περίπτωση, για να εμφανιστεί η εξάρτηση μιας συνάρτησης από το όρισμά της, γράφεται ως "diff(f(x), x) και η ίδια η συνάρτηση είναι f(x).
Παράδειγμα. Βρείτε τη γενική λύση της συνηθισμένης διαφορικής εξίσωσης πρώτης τάξης y" - ax = 0.

Εάν η τιμή της δεξιάς πλευράς της εξίσωσης είναι μηδέν, τότε μπορεί να παραλειφθεί εντελώς. Φυσικά, η δεξιά πλευρά της εξίσωσης μπορεί να περιέχει μια έκφραση.
Όπως μπορείτε να δείτε, κατά την επίλυση διαφορικών εξισώσεων, το Maxima χρησιμοποιεί τη σταθερά ολοκλήρωσης %c, η οποία, από μαθηματική άποψη, είναι μια αυθαίρετη σταθερά που καθορίζεται από πρόσθετες συνθήκες.
Υπάρχει ένας άλλος τρόπος επίλυσης μιας συνηθισμένης διαφορικής εξίσωσης, ο οποίος είναι ευκολότερος για τον χρήστη. Για να το κάνετε αυτό, εκτελέστε την εντολή Εξισώσεις > Επίλυση ODE και εισαγάγετε τα ορίσματα της συνάρτησης ode2 στο παράθυρο Επίλυση ODE.

Το Maxima σας επιτρέπει να λύσετε διαφορικές εξισώσεις δεύτερης τάξης. Η συνάρτηση ode2 χρησιμοποιείται επίσης για αυτό. Για τον προσδιορισμό των παραγώγων σε διαφορικές εξισώσεις, χρησιμοποιείται η συνάρτηση diff, στην οποία προστίθεται ένα ακόμη όρισμα - η σειρά της εξίσωσης: "diff(f(x), x, 2). Για παράδειγμα, η λύση σε ένα συνηθισμένο δευτερόλεπτο- Η διαφορική εξίσωση τάξης a·y"" + b·y" = 0 θα μοιάζει με:

Μαζί με τη συνάρτηση ode2, μπορείτε να χρησιμοποιήσετε τρεις συναρτήσεις, η χρήση των οποίων σας επιτρέπει να βρείτε μια λύση κάτω από ορισμένους περιορισμούς με βάση τη γενική λύση των διαφορικών εξισώσεων που λαμβάνεται από τη συνάρτηση ode2:
- ic1 (αποτέλεσμα της συνάρτησης ode2, αρχική τιμή της ανεξάρτητης μεταβλητής με τη μορφή x = x 0, τιμή της συνάρτησης στο σημείο x 0 στη μορφή y = y 0). Σχεδιασμένο για να λύνει μια διαφορική εξίσωση πρώτης τάξης με αρχικές συνθήκες.
- ic2(αποτέλεσμα της συνάρτησης ode2, αρχική τιμή της ανεξάρτητης μεταβλητής με τη μορφή x = x 0, τιμή της συνάρτησης στο σημείο x 0 με τη μορφή y = y 0, αρχική τιμή για την πρώτη παράγωγο της εξαρτημένης μεταβλητής σε σχέση με το ανεξάρτητη μεταβλητή με τη μορφή (y,x) = dy 0). Σχεδιασμένο για να λύνει μια διαφορική εξίσωση δεύτερης τάξης με αρχικές συνθήκες
- bc2(το αποτέλεσμα της συνάρτησης ode2, η αρχική τιμή της ανεξάρτητης μεταβλητής με τη μορφή x = x 0, η τιμή της συνάρτησης στο σημείο x 0 με τη μορφή y = y 0, η τελική τιμή της ανεξάρτητης μεταβλητής στο μορφή x = x n, η τιμή της συνάρτησης στο σημείο x n με τη μορφή y = y n). Σχεδιασμένο για να λύσει ένα πρόβλημα οριακής τιμής για μια διαφορική εξίσωση δεύτερης τάξης.
Η λεπτομερής σύνταξη αυτών των λειτουργιών βρίσκεται στην τεκμηρίωση του συστήματος.
Ας λύσουμε το πρόβλημα του Cauchy για την εξίσωση πρώτης τάξης y" - ax = 0 με την αρχική συνθήκη y(n) = 1.

Ας δώσουμε ένα παράδειγμα επίλυσης ενός προβλήματος οριακής τιμής για μια διαφορική εξίσωση δεύτερης τάξης y""+y=x με αρχικές συνθήκες y(o) = 0; y(4)=1.

Θα πρέπει να ληφθεί υπόψη ότι αρκετά συχνά το σύστημα δεν μπορεί να λύσει διαφορικές εξισώσεις. Για παράδειγμα, όταν προσπαθούμε να βρούμε μια γενική λύση σε μια συνηθισμένη διαφορική εξίσωση πρώτης τάξης, παίρνουμε:

Σε τέτοιες περιπτώσεις, το Maxima είτε εκδίδει ένα μήνυμα σφάλματος (όπως σε αυτό το παράδειγμα) είτε απλώς επιστρέφει "false".
Μια άλλη επιλογή για την επίλυση συνηθισμένων διαφορικών εξισώσεων πρώτης και δεύτερης τάξης έχει σχεδιαστεί για την εύρεση λύσεων με αρχικές συνθήκες. Υλοποιείται χρησιμοποιώντας τη συνάρτηση κατάργησης.
Σύνταξη συνάρτησης:
desolve (διαφορική εξίσωση, μεταβλητή);
Εάν ένα σύστημα διαφορικών εξισώσεων λύνεται ή υπάρχουν πολλές μεταβλητές, τότε η εξίσωση ή/και οι μεταβλητές παρουσιάζονται με τη μορφή λίστας:
desolve([λίστα εξισώσεων], [variable1, variable2,...]);
Όπως και στην προηγούμενη έκδοση, η συνάρτηση diff χρησιμοποιείται για να δηλώσει παραγώγους σε διαφορικές εξισώσεις, η οποία έχει τη μορφή «diff(f(x), x).
Οι αρχικές τιμές για μια μεταβλητή παρέχονται από τη συνάρτηση atvalue. Αυτή η συνάρτηση έχει την ακόλουθη σύνταξη:
atvalue(συνάρτηση, μεταβλητή = σημείο, τιμή στο σημείο);
Σε αυτήν την περίπτωση, προβλέπεται ότι οι τιμές των συναρτήσεων και (ή) των παραγώγων τους είναι μηδενικές, επομένως η σύνταξη της συνάρτησης atvalue είναι:
atvalue(συνάρτηση, μεταβλητή = 0, τιμή στο σημείο "0");
Παράδειγμα. Βρείτε λύση στη διαφορική εξίσωση πρώτης τάξης y"=sin(x) με την αρχική συνθήκη.

Σημειώστε ότι ακόμη και αν δεν υπάρχει αρχική συνθήκη, η συνάρτηση θα λειτουργήσει και θα παράγει το αποτέλεσμα:

Αυτό επιτρέπει τη δοκιμή της λύσης για μια συγκεκριμένη αρχική τιμή. Πράγματι, αντικαθιστώντας την τιμή y(0) = 4 στο αποτέλεσμα που προκύπτει, παίρνουμε y(x) = 5 - cos(x).
Η συνάρτηση desolve καθιστά δυνατή την επίλυση συστημάτων διαφορικών εξισώσεων με αρχικές συνθήκες.
Ας δώσουμε ένα παράδειγμα επίλυσης συστήματος διαφορικών εξισώσεων  με αρχικές συνθήκες y(0) = 0; z(0) = 1.
με αρχικές συνθήκες y(0) = 0; z(0) = 1.

Επεξεργασία δεδομένων
Στατιστική ανάλυση
Το σύστημα καθιστά δυνατό τον υπολογισμό βασικών στατιστικών περιγραφικών στατιστικών, με τη βοήθεια των οποίων περιγράφονται οι πιο γενικές ιδιότητες των εμπειρικών δεδομένων. Οι βασικές περιγραφικές στατιστικές περιλαμβάνουν τη μέση τιμή, τη διακύμανση, την τυπική απόκλιση, τη διάμεση τιμή, τον τρόπο λειτουργίας, τις μέγιστες και ελάχιστες τιμές, το εύρος διακύμανσης και τα τεταρτημόρια. Οι δυνατότητες του Maxima από αυτή την άποψη είναι κάπως μέτριες, αλλά τα περισσότερα από αυτά τα στατιστικά στοιχεία είναι αρκετά εύκολο να υπολογιστούν με τη βοήθειά του.
Ο ευκολότερος τρόπος για τον υπολογισμό των στατιστικών περιγραφικών στατιστικών είναι να χρησιμοποιήσετε την παλέτα Statistics.

Ο πίνακας περιέχει έναν αριθμό εργαλείων ομαδοποιημένων σε τέσσερις ομάδες.
- Στατιστικοί δείκτες (περιγραφικές στατιστικές):
- μέσος όρος (αριθμητικός μέσος όρος).
- διάμεσος(διάμεσος)
- διακύμανση (variance);
- απόκλιση (τυπική απόκλιση).
- Δοκιμές.
- Κατασκευή πέντε τύπων γραφημάτων:
- ιστόγραμμα. Χρησιμοποιείται κυρίως στις στατιστικές για την απεικόνιση διαστημάτων σειρών διανομών. Κατά την κατασκευή του, τα μέρη ή οι συχνότητες σχεδιάζονται κατά μήκος του άξονα τεταγμένων και οι τιμές του χαρακτηριστικού σχεδιάζονται στον άξονα της τετμημένης.
- διάγραμμα διασποράς (διάγραμμα συσχέτισης, πεδίο συσχέτισης, διάγραμμα διασποράς) - ένα γράφημα σημείων όταν τα σημεία δεν συνδέονται. Χρησιμοποιείται για την εμφάνιση δεδομένων για δύο μεταβλητές, η μία από τις οποίες είναι ένας παράγοντας και η άλλη ένα αποτέλεσμα. Με τη βοήθειά του, πραγματοποιείται μια γραφική αναπαράσταση ζευγών δεδομένων με τη μορφή ενός συνόλου σημείων ("σύννεφα") στο επίπεδο συντεταγμένων.
- Γράφημα ράβδων - ένα γράφημα με τη μορφή κάθετων στηλών.
- τομέα ή γράφημα πίτας (Διάγραμμα πίτας). Ένα τέτοιο διάγραμμα χωρίζεται σε πολλά τμήματα-τομείς, η περιοχή καθενός από τα οποία είναι ανάλογη με το μέρος τους.
- οικόπεδο κουτιού (κουτί με μουστάκι, κουτί με μουστάκι, Οικόπεδο κουτιού, διάγραμμα κουτιού και μουστάκι). Είναι αυτό που χρησιμοποιείται συχνότερα για την εμφάνιση στατιστικών δεδομένων. Οι πληροφορίες σε αυτό το διάγραμμα είναι πολύ κατατοπιστικές και χρήσιμες. Εμφανίζει ταυτόχρονα πολλές τιμές που χαρακτηρίζουν τη σειρά παραλλαγών: ελάχιστες και μέγιστες τιμές, μέσος όρος και διάμεσος, πρώτο και τρίτο τεταρτημόριο.
- Εργαλεία για ανάγνωση ή δημιουργία μήτρας. Για να χρησιμοποιήσετε τα εργαλεία της παλέτας, πρέπει να έχετε αρχικά δεδομένα με τη μορφή μήτρας - μονοδιάστατου πίνακα. Μπορείτε να το δημιουργήσετε στο έγγραφο με την τρέχουσα περίοδο λειτουργίας και στη συνέχεια να αντικαταστήσετε το όνομά του ως είσοδο στα παράθυρα του εργαλείου παλέτας με τον ίδιο τρόπο όπως η επίλυση εξισώσεων χρησιμοποιώντας τον πίνακα Γενικά Μαθηματικά. Μπορείτε επίσης να εισάγετε απευθείας τα δεδομένα στα παράθυρα εισαγωγής δεδομένων. Στην περίπτωση αυτή, εισάγονται με τη μορφή που είναι αποδεκτή στο σύστημα, δηλαδή σε αγκύλες και χωρίζονται με κόμματα. Είναι σαφές ότι η πρώτη επιλογή είναι πολύ καλύτερη, καθώς απαιτεί μόνο μία φορά εισαγωγή δεδομένων.
Εκτός από τον πίνακα, όλα τα στατιστικά εργαλεία μπορούν επίσης να χρησιμοποιηθούν χρησιμοποιώντας τις αντίστοιχες λειτουργίες.
Μαξίμα- ένα σύστημα υπολογιστή που σας επιτρέπει να εργάζεστε με συμβολικές και αριθμητικές εκφράσεις. Υποστηρίζει λειτουργίες επέκτασης σειρών, διαφοροποίησης, μετασχηματισμού Laplace, ολοκλήρωσης. Το πρόγραμμα δεν φοβάται συνηθισμένες διαφορικές εξισώσεις, πίνακες και τανυστές, συστήματα γραμμικών εξισώσεων, λίστες, διανύσματα, πολυώνυμα, σύνολα. Το υπολογιστικό σύστημα μπορεί να παράγει υπολογισμούς με υψηλό βαθμό ακρίβειας. Χρησιμοποιεί ακέραιους και κλασματικές εκφράσεις. Η εφαρμογή μπορεί να δημιουργήσει γραφήματα σε δύο ή τρεις διαστάσεις. Διαθέτει εγχειρίδιο που περιγράφει λεπτομερώς τον τρόπο εργασίας με το βοηθητικό πρόγραμμα, ποιοι χειριστές υποστηρίζονται από το σύστημα μαθηματικών πράξεων. Το πρόγραμμα είναι τέλειο για τους λάτρεις της άλγεβρας υπολογιστών: φοιτητές, καθηγητές, μεταπτυχιακούς φοιτητές.


- Εργάζεται με μαθηματικές αριθμητικές και συμβολικές εκφράσεις.
- Υποστηρίζει εργασία με λίστες, πολυώνυμα, πίνακες, τανυστές, διαφορικές εξισώσεις και συστήματα γραμμικών εξισώσεων.
- Υποστηρίζει λειτουργίες επέκτασης σειρών, διαφοροποίησης, μετασχηματισμού Laplace, ολοκλήρωσης.
- Εκτελεί υπολογισμούς με υψηλό βαθμό ακρίβειας.
- Χρησιμοποιεί ακέραιους αριθμούς, κλασματικές εκφράσεις.
- Δυνατότητα κατασκευής γραφημάτων σε δισδιάστατες ή τρισδιάστατες διαστάσεις.
- Κατάλληλο για τους λάτρεις της άλγεβρας υπολογιστών.
- Διαθέτει προσβάσιμη τεκμηρίωση για εξοικείωση με τη λειτουργία του συστήματος.
- Δεν επηρεάζει την απόδοση και την ταχύτητα του περιβάλλοντος λειτουργίας.
- Υπάρχει υποστήριξη για τη ρωσική γλώσσα.
Μειονεκτήματα του προγράμματος
- Δεν υπάρχει φορητή έκδοση.- Επεξεργαστής με συχνότητα ρολογιού 1200 MHz ή πιο ισχυρό.
- RAM 256 MB ή περισσότερο.
- Ελεύθερος χώρος στον σκληρό δίσκο από 185 MB.
- Αρχιτεκτονική 32-bit ή 64-bit (x86 ή x64).
- Λειτουργικό σύστημα Windows XP, Windows Vista, Windows 7, Windows 8
Υπολογιστές πολλαπλών λειτουργιών: Πίνακες σύγκρισης
| Το όνομα του προγράμματος | Στα ρώσικα | Διανομές | Εγκαταστάτης | Δημοτικότητα | Μέγεθος | Δείκτης |
| ★ ★ ★ ★ ★ | 48,7 MB | 100 | ||||
| ★ ★ ★ ★ ★ | 59,8 MB | 99 | ||||
| ★ ★ ★ ★ ★ | 1,3 MB | 86 | ||||
Το σύστημα Maxima έχει πολλές ενσωματωμένες λειτουργίες. Κάθε ενσωματωμένη λειτουργία μπορεί να περιγραφεί στην τεκμηρίωση που περιέχεται στο σύστημα βοήθειας. Μπορείτε να προσπελάσετε τη βοήθεια χρησιμοποιώντας το πλήκτρο λειτουργίας F1. Το Maxima διαθέτει επίσης μια ειδική λειτουργία που παρέχει πληροφορίες από την τεκμηρίωση για συγκεκριμένες λέξεις. Μια συντομευμένη έκδοση αυτής της κλήσης συνάρτησης: ?? όνομα (Εικ. 12). Εδώ;; είναι το όνομα του τελεστή και το όρισμα πρέπει να διαχωρίζεται από αυτό με ένα κενό. Χειριστής;; εμφανίζει μια λίστα με τις ενότητες βοήθειας και τα ονόματα συναρτήσεων που περιέχουν το καθορισμένο κείμενο, μετά από το οποίο σας ζητούν να εισαγάγετε τον αριθμό της ενότητας ή την περιγραφή της συνάρτησης που θέλετε να δείτε:
Εικ. 12. Κλήση βοήθειας σε μια εντολή ενδιαφέροντος συστήματος Maxima
Σημειώστε ότι στο σύστημα Maxima δεν υπάρχει σαφής διάκριση μεταξύ χειριστή και λειτουργιών. Εξάλλου, κάθε δήλωση είναι στην πραγματικότητα μια συνάρτηση.
Όλες οι λειτουργίες και οι τελεστές Maxima δεν λειτουργούν μόνο με πραγματικούς αριθμούς, αλλά και με μιγαδικούς αριθμούς. Οι ίδιοι οι μιγαδικοί αριθμοί γράφονται σε αλγεβρική μορφή, με τη φανταστική μονάδα να συμβολίζεται με %i. δηλαδή με τη μορφή a+b*%i, όπου ΕΝΑΚαι σιείναι το πραγματικό και το φανταστικό μέρος ενός αριθμού, αντίστοιχα.
Ας σκεφτούμε βασική σύνταξη συνάρτησηςΣυστήματα Maxima.
1. Αριθμητικοί τελεστές: + , -, *, /, -->. Παράδειγμα:

3. Λογικοί τελεστές: και, ή, όχι. Παράδειγμα:

4. Συνάρτηση για την εύρεση του παραγοντικού ενός αριθμού: !
Το παραγοντικό δίνεται στην πιο γενική μορφή και είναι, στην πραγματικότητα, μια συνάρτηση γάμμα (ακριβέστερα, x! = γάμμα(x+1)), δηλαδή ορίζεται στο σύνολο όλων των μιγαδικών αριθμών εκτός από τους αρνητικούς ακεραίους. Το παραγοντικό ενός φυσικού αριθμού (και μηδέν) απλοποιείται αυτόματα στον ίδιο φυσικό αριθμό.
![]()
5. Η συνάρτηση για την εύρεση του ημιπαραγοντικού είναι: !! (το γινόμενο όλων των ζυγών (για έναν άρτιο τελεστή) ή των περιττών αριθμών μικρότερων ή ίσων του δεδομένου).
6. Συνάρτηση άρνησης συντακτικής ισότητας: #Ο συμβολισμός a#b είναι ισοδύναμος με το not a=b. 
7. Συνάρτηση για την εύρεση του συντελεστή ενός αριθμού x: abs(x) Ο συντελεστής ορίζεται για όλους τους μιγαδικούς αριθμούς. Παράδειγμα:

8. Συνάρτηση που επιστρέφει το πρόσημο του αριθμού x: signum(x)

9. Συναρτήσεις που επιστρέφουν τις μεγαλύτερες και τις μικρότερες τιμές δεδομένων πραγματικών αριθμών: max(x1,...,xn) και min(x1,...,xn).

10. Μερικές ενσωματωμένες μαθηματικές συναρτήσεις:
| sqrt(x) | Τετραγωνική ρίζα του x |
| acos(x) | Αρκοζίνη του ορίσματος x |
| acosh (x) | Υπερβολικό τόξο συνημίτονο του x |
| acot(x) | Arccotangent του ορίσματος x |
| acoth (x) | Υπερβολικό τόξο συνεφαπτομένη του ορίσματος x |
| acsc(x) | Arccosecant του ορίσματος x |
| acsch(x) | Υπερβολικό τόξο του ορίσματος x |
| asec(x) | Τοξοτόξο του ορίσματος x |
| asch(x) | Υπερβολικό τόξο του ορίσματος x |
| asin(x) | Αρξίνη του ορίσματος x |
| asinh(x) | Υπερβολικό τόξο του ορίσματος x |
| atan(x) | Arctangent του ορίσματος x |
| atanh (x) | Υπερβολική εφαπτομένη του ορίσματος x |
| cosh(x) | Υπερβολικό συνημίτονο του ορίσματος x |
| coth(x) | Υπερβολική συνεφαπτομένη του ορίσματος x |
| csc(x) | Συνέπεια του επιχειρήματος x |
| csch(x) | Υπερβολική συνέκταση του ορίσματος x |
| sec(x) | Τομή του ορίσματος x |
| sech(x) | Υπερβολική τομή του ορίσματος x |
| αμαρτία (x) | Ημίτονο του x |
| sinh(x) | Υπερβολικό ημίτονο του ορίσματος x |
| μαύρισμα (x) | Εφαπτομένη x |
| tanh(x) | Υπερβολική εφαπτομένη του ορίσματος x |
| ημερολόγιο (x) | Φυσικός λογάριθμος του x |
| exp(x) | Εκθέτης x |
11. Λειτουργίες για εργασία με πίνακες:
ορίζουσα – εύρεση της ορίζουσας ενός πίνακα:
ιδιοτιμές - εύρεση των ιδιοτιμών του πίνακα:
αντιστρέφω– λήψη του αντίστροφου πίνακα:

ανήλικος– ορίζει την ελάσσονα του πίνακα. Το πρώτο όρισμα είναι ένας πίνακας, το δεύτερο και
το τρίτο είναι τα ευρετήρια γραμμής και στήλης, αντίστοιχα:
τάξη– κατάταξη μήτρας:
υπομήτρα– επιστρέφει τη μήτρα που λαμβάνεται από το πρωτότυπο με αφαίρεση
αντίστοιχες γραμμές ή/και στήλες. Οι παράμετροι είναι:
αριθμοί σειρών προς διαγραφή, αρχικός πίνακας, αριθμός στηλών προς διαγραφή.

μεταθέτω– μεταφορά μήτρας:

Η γλώσσα συστήματος Maxima περιέχει τους βασικούς εκτελέσιμους τελεστές που βρίσκονται σε οποιαδήποτε γλώσσα προγραμματισμού. Ας τους δούμε.
Τελεστές εκχώρησης τιμών (παραστάσεις ονομασίας).
1. Operator “:” (τελεστής για τον καθορισμό της τιμής μιας μεταβλητής).
2. Χειριστής “:=” (τελεστής για τον καθορισμό μιας λειτουργίας χρήστη).
3.Εκτεταμένες εκδόσεις των τελεστών εκχώρησης και εκχώρησης συναρτήσεων, που συμβολίζονται αντίστοιχα με:: και::=.
Η χρήση ενός τελεστή συνάρτησης χρήστη κάνει την εργασία με μια συνάρτηση χρήστη πολύ πιο εύκολη, επειδή είναι προσβάσιμη με το όνομα και οι τιμές της συνάρτησης σε δεδομένα σημεία μπορούν να υπολογιστούν εύκολα και εύκολα.
Παράδειγμα: βρείτε την τιμή μιας συνάρτησης φά (x,y)=cosx + αμαρτία yστο σημείο

Χειριστής βρόχου.Ο τελεστής βρόχου μπορεί να καθοριστεί με διάφορους τρόπους. Η μέθοδος καθορισμού εξαρτάται από το εάν είναι γνωστό εκ των προτέρων πόσες φορές πρέπει να εκτελεστεί το σώμα του βρόχου.
Παράδειγμα: Ρύθμιση βρόχου για την εμφάνιση των τιμών μιας μεταβλητής ΕΝΑστην περιοχή από -3 έως 10 σε βήματα των 5:

Το επόμενο σημαντικό χαρακτηριστικό του συστήματος Maxima είναι εργασία με λίστες και πίνακες.
Για να δημιουργήσετε λίστες, χρησιμοποιήστε την εντολή makelist. Για παράδειγμα, χρησιμοποιώντας την εντολή

έχουμε σχηματίσει μια λίστα με το όνομα x, που αποτελείται από δέκα στοιχεία των οποίων οι τιμές βρίσκονται σύμφωνα με τον τύπο.
Για να σχηματίσετε πίνακες, χρησιμοποιήστε την εντολή array. Για παράδειγμα, χρησιμοποιώντας την εντολή,
![]()
έχουμε σχηματίσει έναν δισδιάστατο πίνακα Α που αποτελείται από 10 σειρές και 5 στήλες. Για να γεμίσουμε τον πίνακα με στοιχεία, θα χρησιμοποιήσουμε έναν βρόχο με μια παράμετρο. Για παράδειγμα,
Για να εμφανίσετε στοιχεία πίνακα στην οθόνη, μπορείτε να χρησιμοποιήσετε την εντολή:
Ένας πίνακας μπορεί να σχηματιστεί χωρίς προηγούμενη δήλωση. Στο παρακάτω παράδειγμα, έχουμε σχηματίσει έναν μονοδιάστατο πίνακα x, που αποτελείται από 5 στοιχεία, οι τιμές των οποίων υπολογίζονται χρησιμοποιώντας τον τύπο x( Εγώ)=αμαρτία Εγώ

Η ταλαιπωρία της εργασίας με πίνακες είναι ότι οι τιμές των στοιχείων του πίνακα εμφανίζονται σε μια στήλη. Είναι πολύ πιο βολικό εάν οι τιμές ενός (δισδιάστατου) πίνακα εμφανίζονται ως μήτρα. Για αυτούς τους σκοπούς, μπορείτε να χρησιμοποιήσετε την εντολή genmatrix. Για παράδειγμα, για να δημιουργήσετε έναν δισδιάστατο πίνακα (μήτρα), θα πρέπει να καθορίσετε μια εντολή με την ακόλουθη μορφή:
Ας βγάλουμε τον πίνακα που προκύπτει:

6. Οι απλούστεροι μετασχηματισμοί των εκφράσεων.
Από προεπιλογή, η λειτουργία Αυτόματη απλοποίηση είναι ενεργή στο σύστημα Maxima, δηλ. το σύστημα προσπαθεί να απλοποιήσει την ίδια την εισαγόμενη έκφραση χωρίς καμία εντολή.
Παράδειγμα. Ας υποθέσουμε ότι πρέπει να βρείτε την τιμή της ακόλουθης αριθμητικής παράστασης:
Ας ορίσουμε την έκφραση σύμφωνα με τους κανόνες της γλώσσας του συστήματος Maxima.

Όπως μπορείτε να δείτε, το σύστημα απάντησε με την τιμή της έκφρασης, αν και δεν καθορίσαμε καμία εντολή.
Πώς μπορείτε να αναγκάσετε το σύστημα να βγάζει όχι το αποτέλεσμα, αλλά την ίδια την έκφραση; Για να γίνει αυτό, η συνάρτηση απλοποίησης πρέπει να απενεργοποιηθεί χρησιμοποιώντας την εντολή simp: false$. Τότε παίρνουμε:

Για να ενεργοποιήσετε τη συνάρτηση απλοποίησης, πρέπει να καθορίσετε την εντολή simp:true$. Η συνάρτηση αυτόματης απλοποίησης μπορεί να λειτουργήσει τόσο με αριθμητικές όσο και με ορισμένες μη αριθμητικές εκφράσεις. Για παράδειγμα,

Κατά την εισαγωγή, μπορούμε να αναφερθούμε σε οποιοδήποτε από τα προηγούμενα κελιά με το όνομά του, αντικαθιστώντας το σε οποιεσδήποτε εκφράσεις. Επιπλέον, το τελευταίο κελί εξόδου συμβολίζεται με %, και το τελευταίο κελί εισόδου συμβολίζεται με _. Αυτό σας επιτρέπει να ανατρέξετε στο τελευταίο αποτέλεσμα χωρίς να σας αποσπά η προσοχή από τον αριθμό του. Ωστόσο, τέτοιες κλήσεις σε κελιά δεν πρέπει να γίνονται κατάχρηση, καθώς κατά την επανεκτίμηση ολόκληρου του εγγράφου ή των μεμονωμένων κελιών εισόδου του, ενδέχεται να προκύψει ασυμφωνία μεταξύ των αριθμών κελιών.
Παράδειγμα. Βρείτε την τιμή της έκφρασης και αυξήστε το αποτέλεσμα κατά 5 φορές.

Συνιστάται να χρησιμοποιείτε μεταβλητές αντί για ονόματα κελιών και να εκχωρείτε τα ονόματά τους σε οποιεσδήποτε εκφράσεις. Σε αυτήν την περίπτωση, οποιαδήποτε μαθηματική έκφραση μπορεί να λειτουργήσει ως τιμή της μεταβλητής.
Οι τιμές των ονομάτων μεταβλητών διατηρούνται σε όλη τη διάρκεια της εργασίας με το έγγραφο. Ας θυμηθούμε ότι εάν είναι απαραίτητο να αφαιρεθεί ο ορισμός από μια μεταβλητή, αυτό μπορεί να γίνει χρησιμοποιώντας τη συνάρτηση kill(name), όπου το όνομα είναι το όνομα της έκφρασης που θα καταστραφεί. Επιπλέον, αυτό μπορεί να είναι είτε ένα όνομα που έχει εκχωρηθεί από εσάς είτε οποιοδήποτε κελί εισόδου ή εξόδου. Ομοίως, μπορείτε να διαγράψετε όλη τη μνήμη και να ελευθερώσετε όλα τα ονόματα εισάγοντας την εντολή kill(all) (ή επιλέγοντας το μενού Makhta->Διαγραφή μνήμης(Διαγραφή μνήμης)). Σε αυτήν την περίπτωση, όλα τα κελιά εισόδου/εξόδου θα διαγραφούν και η αρίθμησή τους θα ξεκινήσει ξανά από το ένα.
Η συνάρτηση αυτόματης απλοποίησης δεν είναι πάντα σε θέση να απλοποιήσει μια έκφραση. Εκτός από αυτό, υπάρχει ένας αριθμός εντολών που έχουν σχεδιαστεί για να λειτουργούν με εκφράσεις: ορθολογικές και παράλογες. Ας δούμε μερικά από αυτά.
rat (έκφραση) - μετατρέπει μια ορθολογική έκφραση στην κανονική μορφή: ανοίγει όλες τις αγκύλες, στη συνέχεια φέρνει τα πάντα σε έναν κοινό παρονομαστή, αθροίζει και μειώνει. μετατρέπει όλους τους αριθμούς με πεπερασμένο δεκαδικό συμβολισμό σε ορθολογικούς αριθμούς. Η κανονική μορφή «ακυρώνεται» αυτόματα στην περίπτωση τυχόν μετασχηματισμών που δεν είναι ορθολογικοί
ratsimp (έκφραση) - απλοποιεί μια έκφραση μέσω ορθολογικών μετασχηματισμών. Λειτουργεί επίσης «σε βάθος», δηλαδή τα παράλογα μέρη της έκφρασης δεν θεωρούνται ατομικά, αλλά απλοποιούνται, συμπεριλαμβανομένων όλων των λογικών στοιχείων μέσα σε αυτά
fullratsimp(έκφραση) - μια συνάρτηση για την απλοποίηση μιας ορθολογικής έκφρασης εφαρμόζοντας διαδοχικά τη συνάρτηση ratsimp() στην έκφραση που πέρασε. Λόγω αυτού, η συνάρτηση είναι κάπως πιο αργή από την ratsimp(), αλλά δίνει ένα πιο αξιόπιστο αποτέλεσμα.
επέκταση (έκφραση) - επεκτείνει τις παρενθέσεις σε μια έκφραση σε όλα τα επίπεδα ένθεσης. Σε αντίθεση με τη συνάρτηση ratexpand(), δεν μειώνει τα κλάσματα σε κοινό παρονομαστή.
radcan(έκφραση) - μια συνάρτηση για την απλοποίηση λογαριθμικών, εκθετικών και συναρτήσεων ισχύος με μη ακέραιους ορθολογικούς εκθέτες, δηλαδή ρίζες (ριζικές).
Συχνά, όταν προσπαθείτε να απλοποιήσετε μια έκφραση στο Maxima, στην πραγματικότητα μπορεί μόνο να την κάνει πιο περίπλοκη. Μπορεί να προκύψει αύξηση του αποτελέσματος λόγω του γεγονότος ότι δεν είναι γνωστό ποιες τιμές μπορούν να λάβουν οι μεταβλητές που περιλαμβάνονται στην έκφραση. Για να αποφύγετε αυτό, θα πρέπει να βάλετε περιορισμούς στις τιμές που μπορεί να λάβει μια μεταβλητή. Αυτό γίνεται χρησιμοποιώντας τη συνάρτηση assume(condition). Επομένως, σε ορισμένες περιπτώσεις, το καλύτερο αποτέλεσμα μπορεί να επιτευχθεί συνδυάζοντας το radcan() με το ratsimp() ή το fullratsimp().