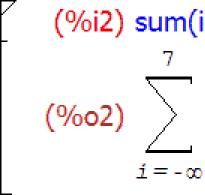Maxima-Beschreibung. Wie man mit Maxima arbeitet
Das Maxima-Mathe-Paket ist einer der besten kostenlosen Ersatz für MathCAD.
Dieses Lehrbuch (im PDF-Format) kann in den Disziplinen Mathematische Analysis, Differentialgleichungen, Anwendungssoftwarepakete usw. in verschiedenen Fachgebieten an Hochschulen verwendet werden, wenn der staatliche Bildungsstandard das Studium des Abschnitts „Differential“ vorsieht Gleichungen“ sowie in Wahlpflichtfächern. Es kann auch nützlich sein, um Computer-Mathematik-Systeme in Fachklassen allgemeinbildender Bildungseinrichtungen mit vertieftem Studium der Mathematik und Informatik kennenzulernen.
- Vorwort
- Kapitel 1. Grundlagen der Arbeit im Maxima-Computermathematiksystem
- 1.1. Über das Maxima-System
- 1.2. Maxima auf einem PC installieren
- 1.3. Maxima-Hauptfensteroberfläche
- 1.4. Arbeiten mit Zellen in Maxima
- 1.5. Arbeiten mit dem Maxima-Hilfesystem
- 1.6. Funktionen und Befehle des Maxima-Systems
- 1.7. Verwalten des Berechnungsprozesses in Maxima
- 1.8. Einfache Ausdruckstransformationen
- 1.9. Lösen algebraischer Gleichungen und ihrer Systeme
- 1.10. Grafikfunktionen
- Kapitel 2. Numerische Methoden zur Lösung von Differentialgleichungen
- 2.1. Allgemeine Informationen zu Differentialgleichungen
- 2.2. Numerische Methoden zur Lösung des Cauchy-Problems für eine gewöhnliche Differentialgleichung erster Ordnung
- 2.2.1. Euler-Methode
- 2.2.2. Euler-Cauchy-Methode
- 2.2.3. Runge-Kutta-Methode 4 Genauigkeitsstufen
- 2.3. Lösen von Randwertproblemen für gewöhnliche Differentialgleichungen mithilfe der Finite-Differenzen-Methode
- 2.4. Gittermethode zur Lösung partieller Differentialgleichungen
- Kapitel 3. Lösungen für Differentialgleichungen im Maxima-System finden
- 3.1. Integrierte Funktionen zum Finden von Lösungen für Differentialgleichungen
- 3.2. Differentialgleichungen und ihre Systeme in symbolischer Form lösen
- 3.3. Konstruktion von Trajektorien und Richtungsfeldern von Differentialgleichungen.
- 3.4. Implementierung numerischer Methoden zur Lösung des Cauchy-Problems für gewöhnliche Differentialgleichungen
- 3.4.1. Euler-Methode
- 3.4.2. Euler-Cauchy-Methode
- 3.4.3. Runge-Kutta-Methode
- 3.5. Implementierung einer Finite-Differenzen-Methode zur Lösung eines Randwertproblems für gewöhnliche Differentialgleichungen
- 3.6. Implementierung der Gittermethode für partielle Differentialgleichungen
- Aufgaben zur eigenständigen Lösung
- Literatur
Vorwort
Die Theorie der Differentialgleichungen ist einer der größten Zweige der modernen Mathematik. Eines der Hauptmerkmale von Differentialgleichungen ist der direkte Zusammenhang zwischen der Theorie der Differentialgleichungen und Anwendungen. Bei der Untersuchung eines physikalischen Phänomens erstellt der Forscher zunächst seine mathematische Idealisierung oder sein mathematisches Modell und schreibt die Grundgesetze, die dieses Phänomen regeln, in mathematischer Form nieder. Sehr oft können diese Gesetze in Form von Differentialgleichungen ausgedrückt werden. Dabei handelt es sich um Modelle verschiedener Phänomene der Kontinuumsmechanik, chemischer Reaktionen, elektrischer und magnetischer Phänomene usw. Durch das Studium der resultierenden Differentialgleichungen zusammen mit zusätzlichen Bedingungen, die in der Regel in Form von Anfangs- und Randbedingungen angegeben werden , erhält der Mathematiker Informationen über das auftretende Phänomen und kann manchmal seine Vergangenheit und Zukunft herausfinden.
Um ein mathematisches Modell in Form von Differentialgleichungen zu erstellen, müssen Sie in der Regel nur lokale Zusammenhänge kennen und benötigen keine Informationen über das gesamte physikalische Phänomen als Ganzes. Ein mathematisches Modell ermöglicht es, ein Phänomen als Ganzes zu untersuchen, seine Entwicklung vorherzusagen und qualitative Bewertungen der darin auftretenden Messungen im Zeitverlauf vorzunehmen. Elektromagnetische Wellen wurden auf der Grundlage der Analyse von Differentialgleichungen entdeckt.
Man kann sagen, dass die Notwendigkeit, Differentialgleichungen für die Bedürfnisse der Mechanik zu lösen, also Bewegungsbahnen zu finden, wiederum für Newton den Anstoß gab, eine neue Analysis zu entwickeln. Die Anwendung der neuen Analysis auf Probleme der Geometrie und Mechanik erfolgte durch gewöhnliche Differentialgleichungen.
Unter Berücksichtigung der modernen Entwicklung der Computertechnologie und der intensiven Entwicklung einer neuen Richtung – Computermathematik – sind Softwarepakete namens Computermathematiksysteme weit verbreitet und gefragt.
Computermathematik ist eine neue Richtung in Wissenschaft und Bildung, die an der Schnittstelle zwischen grundlegender Mathematik, Informations- und Computertechnologien entstanden ist. Ein Computer-Mathematik-System (SCM) ist eine Reihe von Programmen, die eine automatisierte, technologisch einheitliche und geschlossene Verarbeitung mathematischer Probleme bei der Festlegung von Bedingungen in einer speziell entwickelten Sprache ermöglichen.
Moderne Computer-Mathematiksysteme sind Programme mit einer grafischen Mehrfensteroberfläche und einem entwickelten Hilfesystem, das das Erlernen und Verwenden erleichtert. Die Haupttrends in der Entwicklung von SCM sind das Wachstum der mathematischen Fähigkeiten, insbesondere im Bereich der analytischen und symbolischen Berechnungen, eine deutliche Erweiterung der Visualisierungstools für alle Berechnungsstufen, die weit verbreitete Verwendung von 2D- und 3D-Grafiken sowie die Integration verschiedener Systeme untereinander und mit anderer Software, umfassender Zugang zum Internet, Organisation der Zusammenarbeit bei Bildungs- und Wissenschaftsprojekten im Internet, Verwendung von Animations- und Bildverarbeitungstools, Multimedia-Tools usw.
Ein wesentlicher Umstand, der bis vor kurzem den weit verbreiteten Einsatz von SCM im Bildungsbereich verhinderte, sind die hohen Kosten professioneller wissenschaftlich-mathematischer Software. In letzter Zeit stellen jedoch viele Unternehmen, die solche Programme entwickeln und vertreiben, (über das Internet - http://www.softline.ru) frühere Versionen ihrer Programme zur kostenlosen Nutzung zur Verfügung, nutzen in großem Umfang ein Rabattsystem für Bildungseinrichtungen und vertreiben Demo- oder Demoversionen Testversionen für kostenlose Programme
Darüber hinaus erscheinen kostenlose Analoga von Computermathematiksystemen, beispielsweise Maxima, Scilab, Octave usw.
In diesem Tutorial werden die Fähigkeiten des Maxima-Computermathematiksystems zum Finden von Lösungen für Differentialgleichungen untersucht.
Warum Maxima?
Erstens ist das Maxima-System ein gemeinnütziges Open-Source-Projekt. Maxima gehört zu einer Klasse von Softwareprodukten, die unter der GNU GPL (General Public License) vertrieben werden.Zweitens ist Maxima ein Programm zur Lösung mathematischer Probleme sowohl in numerischer als auch in symbolischer Form. Das Spektrum seiner Fähigkeiten ist sehr breit: Aktionen zur Transformation von Ausdrücken, Arbeiten mit Teilen von Ausdrücken, Lösen von Problemen der linearen Algebra, mathematische Analyse, Kombinatorik, Zahlentheorie, Tensoranalyse, statistische Probleme, Konstruktion von Funktionsgraphen in der Ebene und im Raum in verschiedenen Koordinatensystemen usw. d.
Drittens verfügt Maxima jetzt über eine leistungsstarke, effiziente und benutzerfreundliche plattformübergreifende GUI namens WxMaxima (http://wxmaxima.sourceforge.net).
Die Autoren des Buches beschäftigen sich seit zehn Jahren mit Computermathematiksystemen wie Mathematica, Maple, MathCad. Da ich die Fähigkeiten dieser Softwareprodukte kannte, insbesondere zum Finden von Lösungen für Differentialgleichungen, wollte ich daher das Problem der Organisation von Berechnungen in symbolischer Form in frei verteilten Computermathematiksystemen untersuchen.
In diesem Handbuch geht es um die Möglichkeiten, den Prozess der Lösungssuche für Differentialgleichungen auf Basis des Maxima-Systems zu organisieren, und enthält allgemeine Informationen zur Organisation der Arbeit im System.
Das Handbuch besteht aus 3 Kapiteln. Das erste Kapitel führt die Leser in die grafische Benutzeroberfläche wxMaxima des Maxima-Systems, die Funktionen zum Arbeiten darin und die Syntax der Systemsprache ein. Die Betrachtung des Systems beginnt damit, wo Sie die Systemverteilung finden und wie Sie sie installieren. Im zweiten Kapitel werden allgemeine Fragen der Theorie der Differentialgleichungen und numerische Methoden zu deren Lösung erörtert.
Das dritte Kapitel ist den integrierten Funktionen des Maxima-Computermathematiksystems zum Finden von Lösungen für gewöhnliche Differentialgleichungen 1. und 2. Ordnung in symbolischer Form gewidmet. Ebenfalls im dritten Kapitel wird die Implementierung numerischer Methoden zur Lösung von Differentialgleichungen im Maxima-System gezeigt. Am Ende des Handbuchs finden Sie Aufgaben zur eigenständigen Lösung.
Wir hoffen, dass sich ein breites Spektrum von Benutzern für das Handbuch interessiert und es zu ihrem Assistenten bei der Beherrschung eines neuen Werkzeugs zur Lösung mathematischer Probleme wird.
T.N. Gubina, E.V. Andropowa
Yelets, Juli 2009
P.S. Schneller Start: Befehle auszuführen und Funktionen in mwMaxima müssen Sie zuerst den Befehl selbst eingeben und dann Strg+Eingabe drücken.
Operationen der mathematischen Analyse
Beträge
Die Summenfunktion wird verwendet, um Summen zu finden. Funktionssyntax:
Summe (Ausdruck, Variable, untere Grenze der Variablenänderung, obere Grenze der Variablenänderung)
Zum Beispiel:
Wenn Sie dem letzten Argument den Wert der Systemvariablen positive infinity „inf“ zuweisen, zeigt dies das Fehlen einer Obergrenze an und es wird eine unendliche Summe berechnet. Außerdem wird eine unendliche Summe berechnet, wenn Sie dem Argument „untere Grenze der Variablenänderung“ den Wert der negativ unendlichen Systemvariablen „minf“ zuweisen. Die gleichen Werte werden in anderen mathematischen Analysefunktionen verwendet.
Zum Beispiel:

Funktioniert
Um endliche und unendliche Produkte zu finden, verwenden Sie die Produktfunktion. Sie hat die gleichen Argumente wie die Summenfunktion.
Zum Beispiel:

Grenzen
Um Grenzen zu finden, wird die Limit-Funktion verwendet.
Funktionssyntax:
limit(Ausdruck, Variable, Haltepunkt)
Wenn das Argument „breakpoint“ auf „inf“ gesetzt ist, weist dies auf das Fehlen eines Rahmens hin.
Zum Beispiel:

Um einseitige Grenzen zu berechnen, wird ein zusätzliches Argument verwendet, das für die Berechnung der Grenzen rechts den Wert Plus und für links den Wert Minus hat.
Betrachten wir zum Beispiel die Stetigkeit der Funktion arctan(1/(x - 4)). Diese Funktion ist am Punkt x = 4 undefiniert. Berechnen wir die Grenzen rechts und links:

Wie wir sehen können, ist der Punkt x = 4 ein Unstetigkeitspunkt erster Art für diese Funktion, da es links und rechts Grenzen gibt, die gleich -PI/2 bzw. PI/2 sind.
Differenziale
Die Diff-Funktion wird verwendet, um Differenzen zu finden. Funktionssyntax:
diff(Ausdruck, Variable1, Reihenfolge der Ableitung für Variable1 [,Variable2, Reihenfolge der Ableitung für Variable2,...])
Dabei ist der Ausdruck die Funktion, die differenziert wird, das zweite Argument ist die Variable, bezüglich derer die Ableitung vorgenommen werden muss, das dritte (optional) ist die Ordnung der Ableitung (standardmäßig die erste Ordnung).
Zum Beispiel:

Im Allgemeinen ist für die Diff-Funktion nur das erste Argument erforderlich. In diesem Fall gibt die Funktion das Differential des Ausdrucks zurück. Das Differential der entsprechenden Variablen wird mit del(Variablenname) bezeichnet:

Wie wir aus der Syntax der Funktion ersehen können, hat der Benutzer die Möglichkeit, gleichzeitig mehrere Differenzierungsvariablen zu definieren und die Reihenfolge für jede von ihnen festzulegen:

Wenn Sie eine parametrische Funktion verwenden, ändert sich die Schreibweise der Funktion: Nach dem Funktionsnamen werden die Symbole „:=“ geschrieben und der Zugriff auf die Funktion erfolgt über ihren Namen mit einem Parameter:

Die Ableitung kann an einem bestimmten Punkt berechnet werden. Das geht so:

Die Diff-Funktion wird auch zur Bezeichnung von Ableitungen in Differentialgleichungen verwendet, wie unten erläutert.
Integrale
Um Integrale im System zu finden, wird die Integrate-Funktion verwendet. Um das unbestimmte Integral einer Funktion zu finden, werden zwei Argumente verwendet: der Name der Funktion und die Variable, über die die Integration erfolgt. Zum Beispiel:

Wenn die Antwort nicht eindeutig ist, stellt Maxima möglicherweise eine zusätzliche Frage:
Die Antwort muss den Text der Frage enthalten. Wenn in diesem Fall der Wert der Variablen y größer als „0“ ist, ist er „positiv“ und andernfalls „negativ“. In diesem Fall kann nur der erste Buchstabe des Wortes eingegeben werden.
Um ein bestimmtes Integral in einer Funktion zu finden, müssen Sie zusätzliche Argumente angeben: Grenzen des Integrals:
Maxima ermöglicht auch unendliche Integrationsgrenzen. Dazu werden für das dritte und vierte Argument der Funktion die Werte „-inf“ und „inf“ verwendet:

Um den ungefähren Wert des Integrals in numerischer Form zu finden, sollten Sie, wie bereits erwähnt, das Ergebnis in der Ausgabezelle auswählen, das Kontextmenü darauf aufrufen und dort den Eintrag „To Float“ auswählen (in eine Gleitkommazahl umwandeln). .

Das System ist auch in der Lage, mehrere Integrale zu berechnen. Dazu werden Integrate-Funktionen ineinander verschachtelt. Im Folgenden finden Sie Beispiele für die Berechnung des doppelt unbestimmten Integrals und des doppelt bestimmten Integrals:

Lösungen von Differentialgleichungen
Hinsichtlich seiner Fähigkeiten zur Lösung von Differentialgleichungen ist Maxima beispielsweise Maple deutlich unterlegen. Mit Maxima können Sie jedoch weiterhin gewöhnliche Differentialgleichungen erster und zweiter Ordnung sowie deren Systeme lösen. Hierzu werden je nach Zweck zwei Funktionen genutzt. Zur allgemeinen Lösung gewöhnlicher Differentialgleichungen wird die Funktion ode2 verwendet, und zum Finden von Lösungen für Gleichungen oder Gleichungssysteme basierend auf Anfangsbedingungen wird die Funktion desolve verwendet.
Die ode2-Funktion hat die folgende Syntax:
ode2(Gleichung, abhängige Variable, unabhängige Variable);
Die Diff-Funktion wird zur Darstellung von Ableitungen in Differentialgleichungen verwendet. Um jedoch in diesem Fall die Abhängigkeit einer Funktion von ihrem Argument anzuzeigen, wird sie als „diff(f(x), x) geschrieben, und die Funktion selbst ist f(x).
Beispiel. Finden Sie die allgemeine Lösung der gewöhnlichen Differentialgleichung erster Ordnung y" - ax = 0.

Wenn der Wert der rechten Seite der Gleichung Null ist, kann er ganz weggelassen werden. Natürlich kann die rechte Seite der Gleichung einen Ausdruck enthalten.
Wie Sie sehen, verwendet Maxima beim Lösen von Differentialgleichungen die Integrationskonstante %c, die aus mathematischer Sicht eine willkürliche Konstante ist, die aus zusätzlichen Bedingungen bestimmt wird.
Es gibt eine andere Möglichkeit, eine gewöhnliche Differentialgleichung zu lösen, die für den Benutzer einfacher ist. Führen Sie dazu den Befehl Gleichungen > ODE lösen aus und geben Sie die Argumente der Funktion ode2 in das Fenster ODE lösen ein.

Mit Maxima können Sie Differentialgleichungen zweiter Ordnung lösen. Hierzu wird auch die Funktion ode2 verwendet. Um Ableitungen in Differentialgleichungen zu bezeichnen, wird die Diff-Funktion verwendet, bei der ein weiteres Argument hinzugefügt wird – die Reihenfolge der Gleichung: „diff(f(x), x, 2). Beispielsweise ist die Lösung einer gewöhnlichen zweiten- Ordnung Differentialgleichung a·y"" + b·y" = 0 wird wie folgt aussehen:

Zusammen mit der Funktion ode2 können Sie drei Funktionen verwenden, deren Verwendung es Ihnen ermöglicht, unter bestimmten Einschränkungen eine Lösung basierend auf der allgemeinen Lösung von Differentialgleichungen zu finden, die durch die Funktion ode2 erhalten wird:
- ic1 (Ergebnis der Funktion ode2, Anfangswert der unabhängigen Variablen in der Form x = x 0, Wert der Funktion am Punkt x 0 in der Form y = y 0). Entwickelt, um eine Differentialgleichung erster Ordnung mit Anfangsbedingungen zu lösen.
- ic2(Ergebnis der Funktion ode2, Anfangswert der unabhängigen Variablen in der Form x = x 0, Wert der Funktion am Punkt x 0 in der Form y = y 0, Anfangswert für die erste Ableitung der abhängigen Variablen relativ zu unabhängige Variable in der Form (y,x) = dy 0). Entwickelt, um eine Differentialgleichung zweiter Ordnung mit Anfangsbedingungen zu lösen
- bc2(Ergebnis der Funktion ode2, Anfangswert der unabhängigen Variablen in der Form x = x 0, Wert der Funktion am Punkt x 0 in der Form y = y 0, Endwert der unabhängigen Variablen in der Form x = x n, Wert der Funktion am Punkt x n in der Form y = y n). Entwickelt, um ein Randwertproblem für eine Differentialgleichung zweiter Ordnung zu lösen.
Die detaillierte Syntax dieser Funktionen finden Sie in der Systemdokumentation.
Lösen wir das Cauchy-Problem für die Gleichung erster Ordnung y" - ax = 0 mit der Anfangsbedingung y(n) = 1.

Geben wir ein Beispiel für die Lösung eines Randwertproblems für eine Differentialgleichung zweiter Ordnung y""+y=x mit den Anfangsbedingungen y(o) = 0; y(4)=1.

Es ist zu beachten, dass das System häufig keine Differentialgleichungen lösen kann. Wenn wir beispielsweise versuchen, eine allgemeine Lösung für eine gewöhnliche Differentialgleichung erster Ordnung zu finden, erhalten wir:

In solchen Fällen gibt Maxima entweder eine Fehlermeldung aus (wie in diesem Beispiel) oder gibt einfach „false“ zurück.
Eine weitere Möglichkeit zur Lösung gewöhnlicher Differentialgleichungen erster und zweiter Ordnung besteht darin, Lösungen mit Anfangsbedingungen zu finden. Die Implementierung erfolgt mithilfe der Desolve-Funktion.
Funktionssyntax:
auflösen(Differentialgleichung, Variable);
Wenn ein System von Differentialgleichungen gelöst wird oder mehrere Variablen vorhanden sind, werden die Gleichung und/oder die Variablen in Form einer Liste dargestellt:
desolve([Liste der Gleichungen], [Variable1, Variable2,...]);
Wie in der vorherigen Version wird die Diff-Funktion zur Bezeichnung von Ableitungen in Differentialgleichungen verwendet, die die Form „diff(f(x), x)“ hat.
Anfangswerte für eine Variable werden von der Funktion atvalue bereitgestellt. Diese Funktion hat die folgende Syntax:
atvalue(function, variable = point, value at point);
In diesem Fall ist vorgesehen, dass die Werte von Funktionen und (oder) deren Ableitungen auf Null gesetzt werden, daher lautet die Syntax der atvalue-Funktion:
atvalue(function, variable = 0, value at point „0“);
Beispiel. Finden Sie eine Lösung der Differentialgleichung erster Ordnung y"=sin(x) mit der Anfangsbedingung.

Beachten Sie, dass die Funktion auch dann funktioniert, wenn keine Anfangsbedingung vorliegt, und das Ergebnis liefert:

Dadurch kann die Lösung auf einen bestimmten Anfangswert getestet werden. Wenn wir tatsächlich den Wert y(0) = 4 in das resultierende Ergebnis einsetzen, erhalten wir y(x) = 5 - cos(x).
Die Desolve-Funktion ermöglicht die Lösung von Differentialgleichungssystemen mit Anfangsbedingungen.
Lassen Sie uns ein Beispiel für die Lösung eines Systems von Differentialgleichungen geben  mit Anfangsbedingungen y(0) = 0; z(0) = 1.
mit Anfangsbedingungen y(0) = 0; z(0) = 1.

Datenverarbeitung
statistische Analyse
Das System ermöglicht die Berechnung grundlegender statistischer deskriptiver Statistiken, mit deren Hilfe die allgemeinsten Eigenschaften empirischer Daten beschrieben werden. Zu den grundlegenden deskriptiven Statistiken gehören Mittelwert, Varianz, Standardabweichung, Median, Modus, Maximal- und Minimalwerte, Variationsbereich und Quartile. Die diesbezüglichen Fähigkeiten von Maxima sind eher bescheiden, aber die meisten dieser Statistiken lassen sich mit seiner Hilfe recht einfach berechnen.
Der einfachste Weg, statistische deskriptive Statistiken zu berechnen, ist die Verwendung der Statistikpalette.

Das Panel enthält eine Reihe von Werkzeugen, die in vier Gruppen gruppiert sind.
- Statistische Indikatoren (deskriptive Statistik):
- Mittelwert (arithmetisches Mittel);
- Median(Median);
- Varianz (Varianz);
- Abweichung (Standardabweichung).
- Tests.
- Konstruktion von fünf Arten von Diagrammen:
- Histogramm. Es wird vor allem in der Statistik zur Darstellung von Intervallreihen von Verteilungen verwendet. Während seiner Konstruktion werden Teile oder Frequenzen entlang der Ordinatenachse und die Werte des Attributs auf der Abszissenachse aufgetragen.
- Streudiagramm (Korrelationsdiagramm, Korrelationsfeld, Streudiagramm) – ein Diagramm von Punkten, wenn die Punkte keine Verbindung herstellen. Wird verwendet, um Daten für zwei Variablen anzuzeigen, von denen eine ein Faktor und die andere ein Ergebnis ist. Mit seiner Hilfe erfolgt eine grafische Darstellung von Datenpaaren in Form einer Punktmenge („Wolken“) auf der Koordinatenebene;
- Balkendiagramm – ein Diagramm in Form vertikaler Säulen;
- Sektor- oder Tortendiagramm (Pie Chart). Ein solches Diagramm ist in mehrere Segmentsektoren unterteilt, deren Fläche jeweils proportional zu ihrem Teil ist;
- Boxplot (Box mit Whisker, Box mit Whisker, Boxplot, Box-and-Whisker-Diagramm). Es wird am häufigsten zur Anzeige statistischer Daten verwendet. Die Informationen in dieser Tabelle sind sehr informativ und nützlich. Es zeigt gleichzeitig mehrere Werte an, die die Variationsreihe charakterisieren: Minimal- und Maximalwerte, Durchschnitt und Median, erstes und drittes Quartil.
- Werkzeuge zum Lesen oder Erstellen einer Matrix. Um die Palettenwerkzeuge verwenden zu können, benötigen Sie Ausgangsdaten in Form einer Matrix – einem eindimensionalen Array. Sie können es in der aktuellen Sitzung im Dokument erstellen und anschließend seinen Namen als Eingabe in den Paletten-Werkzeugfenstern ersetzen, genauso wie beim Lösen von Gleichungen mit dem Bedienfeld „Allgemeine Mathematik“. Sie können die Daten auch direkt in die Eingabedateneingabefenster eingeben. Die Eingabe erfolgt in diesem Fall in der im System akzeptierten Form, also in eckigen Klammern und durch Komma getrennt. Es ist klar, dass die erste Option viel besser ist, da sie nur eine einmalige Dateneingabe erfordert.
Neben dem Panel können auch alle Statistiktools über die entsprechenden Funktionen genutzt werden.
Maxima- ein Computersystem, das Ihnen die Arbeit mit symbolischen und numerischen Ausdrücken ermöglicht. Unterstützt Operationen der Reihenerweiterung, Differenzierung, Laplace-Transformation und Integration. Das Programm hat keine Angst vor gewöhnlichen Differentialgleichungen, Matrizen und Tensoren, linearen Gleichungssystemen, Listen, Vektoren, Polynomen und Mengen. Das Computer-Rechensystem kann Berechnungen mit einem hohen Maß an Genauigkeit durchführen. Verwendet ganze Zahlen und gebrochene Ausdrücke. Die Anwendung kann Diagramme in zwei oder drei Dimensionen erstellen. Es gibt ein Handbuch, das detailliert beschreibt, wie man mit dem Dienstprogramm arbeitet und welche Operatoren das System mathematischer Operationen unterstützt. Das Programm ist perfekt für Computeralgebra-Liebhaber: Studenten, Lehrer, Doktoranden.


- Funktioniert mit mathematischen, numerischen und symbolischen Ausdrücken.
- Unterstützt die Arbeit mit Listen, Polynomen, Matrizen, Tensoren, Differentialgleichungen und linearen Gleichungssystemen.
- Unterstützt Operationen der Reihenerweiterung, Differenzierung, Laplace-Transformation und Integration.
- Führt Berechnungen mit einem hohen Maß an Genauigkeit durch.
- Verwendet ganze Zahlen und gebrochene Ausdrücke.
- Kann Diagramme in zweidimensionalen oder dreidimensionalen Dimensionen erstellen.
- Geeignet für Fans der Computeralgebra.
- Verfügt über eine zugängliche Dokumentation, um sich mit der Funktionsweise des Systems vertraut zu machen.
- Beeinträchtigt nicht die Leistung und Geschwindigkeit der Betriebsumgebung.
- Es gibt Unterstützung für die russische Sprache.
Nachteile des Programms
- Es gibt keine tragbare Version.- Prozessor mit einer Taktfrequenz von 1200 MHz oder leistungsfähiger.
- RAM 256 MB oder mehr.
- Freier Festplattenspeicher ab 185 MB.
- 32-Bit- oder 64-Bit-Architektur (x86 oder x64).
- Operationssystem Windows XP, Windows Vista, Windows 7, Windows 8
Multifunktionsrechner: Vergleichstabellen
| Der Name des Programms | Auf Russisch | Verteilungen | Installateur | Popularität | Größe | Index |
| ★ ★ ★ ★ ★ | 48,7 MB | 100 | ||||
| ★ ★ ★ ★ ★ | 59,8 MB | 99 | ||||
| ★ ★ ★ ★ ★ | 1,3 MB | 86 | ||||
Das Maxima-System verfügt über viele integrierte Funktionen. Jede integrierte Funktion kann in der Dokumentation im Hilfesystem beschrieben werden. Die Hilfe kann über die Funktionstaste F1 aufgerufen werden. Maxima verfügt außerdem über eine spezielle Funktion, die für bestimmte Wörter Informationen aus der Dokumentation bereitstellt. Eine verkürzte Version dieses Funktionsaufrufs: ?? Namen (Abb. 12). Hier?? ist der Name des Operators und das Argument muss durch ein Leerzeichen von ihm getrennt werden. Operator?? zeigt eine Liste der Hilfeabschnitte und Funktionsnamen an, die den angegebenen Text enthalten. Anschließend werden Sie aufgefordert, die Nummer des Abschnitts oder die Beschreibung der Funktion einzugeben, die Sie anzeigen möchten:
Abb. 12. Rufen Sie Hilfe zu einem Maxima-Systembefehl auf, der Sie interessiert
Beachten Sie, dass es im Maxima-System keine klare Unterscheidung zwischen Operatoren und Funktionen gibt. Außerdem, Jede Aussage ist eigentlich eine Funktion.
Alle Maxima-Funktionen und -Operatoren funktionieren nicht nur mit reellen Zahlen, sondern auch mit komplexen Zahlen. Die komplexen Zahlen selbst werden in algebraischer Form geschrieben, wobei die imaginäre Einheit mit %i bezeichnet wird; das heißt, in der Form a+b*%i, wobei A Und B sind der Real- bzw. Imaginärteil einer Zahl.
Lassen Sie uns überlegen grundlegende Funktionssyntax Maxima-Systeme.
1. Arithmetische Operatoren: + , -, *, /, -->. Beispiel:

3. Logische Operatoren: und, oder, nicht. Beispiel:

4. Funktion zum Finden der Fakultät einer Zahl: !
Die Fakultät wird in der allgemeinsten Form angegeben und ist tatsächlich eine Gammafunktion (genauer gesagt x! = gamma(x+1)), das heißt, sie ist auf der Menge aller komplexen Zahlen außer negativen ganzen Zahlen definiert. Die Fakultät einer natürlichen Zahl (und Null) vereinfacht sich automatisch zu derselben natürlichen Zahl.
![]()
5. Die Funktion zum Finden der Semifaktorie lautet: !! (das Produkt aller geraden (für einen geraden Operanden) oder ungeraden Zahlen, die kleiner oder gleich der angegebenen sind).
6. Syntaktische Gleichheitsnegationsfunktion: # Notation a#b ist äquivalent zu not a=b. Beispiel: 
7. Funktion zum Ermitteln des Moduls einer Zahl x: abs(x) Der Modul ist für alle komplexen Zahlen definiert. Beispiel:

8. Funktion, die das Vorzeichen der Zahl x zurückgibt: signum(x)

9. Funktionen, die den größten und kleinsten Wert gegebener reeller Zahlen zurückgeben: max(x1,...,xn) und min(x1,...,xn).

10. Einige integrierte mathematische Funktionen:
| sqrt(x) | Quadratwurzel von x |
| acos(x) | Arkuskosinus des Arguments x |
| Acosh (x) | Hyperbolischer Arcuscosinus von x |
| acot(x) | Arckotangens des Arguments x |
| acoth (x) | Hyperbolischer Bogenkotangens des Arguments x |
| acsc(x) | Arckosekans des Arguments x |
| acsch(x) | Hyperbolischer Arkuskosekans des Arguments x |
| asec(x) | Arcsecant des Arguments x |
| asech(x) | Hyperbolischer Arcsecans des Arguments x |
| asin(x) | Arkussinus des Arguments x |
| asinh(x) | Hyperbolischer Arkussinus des Arguments x |
| atan(x) | Arkustangens des Arguments x |
| atanh (x) | Hyperbolischer Arkustangens des Arguments x |
| cosh(x) | Hyperbolischer Kosinus des Arguments x |
| coth(x) | Hyperbolischer Kotangens des Arguments x |
| csc(x) | Kosekans des Arguments x |
| csch(x) | Hyperbolischer Kosekans des Arguments x |
| Sek(x) | Sekante des Arguments x |
| sech(x) | Hyperbolischer Sekante des Arguments x |
| Sünde(x) | Sinus von x |
| sinh(x) | Hyperbolischer Sinus des Arguments x |
| tan(x) | Tangente x |
| tanh(x) | Hyperbolischer Tangens des Arguments x |
| log(x) | Natürlicher Logarithmus von x |
| exp(x) | Exponent x |
11. Funktionen zum Arbeiten mit Matrizen:
Determinante – Bestimmung der Determinante einer Matrix:
Eigenwerte – Finden der Eigenwerte der Matrix:
umkehren– Erhalten der inversen Matrix:

unerheblich– definiert das Moll der Matrix. Das erste Argument ist eine Matrix, das zweite und
Der dritte sind die Zeilen- bzw. Spaltenindizes:
Rang– Matrixrang:
Untermatrix– gibt die durch Entfernen aus dem Original erhaltene Matrix zurück
entsprechenden Zeilen und/oder Spalten. Die Parameter sind:
Anzahl der zu löschenden Zeilen, Originalmatrix, Anzahl der zu löschenden Spalten.

transponieren– Matrixtransposition:

Die Maxima-Systemsprache enthält die grundlegenden ausführbaren Operatoren, die in jeder Programmiersprache zu finden sind. Schauen wir sie uns an.
Wertzuweisungsoperatoren (Benennungsausdrücke).
1. Operator „:“ (Operator zum Setzen des Wertes einer Variablen).
2. Operator „:=“ (Operator zur Angabe einer Benutzerfunktion).
3.Erweiterte Versionen von Zuweisungs- und Funktionszuweisungsoperatoren, jeweils gekennzeichnet durch:: und::=.
Die Verwendung eines Benutzerfunktionsoperators erleichtert die Arbeit mit einer Benutzerfunktion erheblich, da über den Namen auf sie zugegriffen werden kann und die Werte der Funktion an bestimmten Punkten einfach und bequem berechnet werden können.
Beispiel: Finden Sie den Wert einer Funktion F (x,y)=cosx + sin j am Punkt

Schleifenoperator. Der Schleifenoperator kann auf verschiedene Arten angegeben werden. Die Art der Angabe hängt davon ab, ob im Voraus bekannt ist, wie oft der Schleifenkörper ausgeführt werden muss.
Beispiel: Einrichten einer Schleife zur Anzeige der Werte einer Variablen A im Bereich von -3 bis 10 in 5er-Schritten:

Das nächste wichtige Merkmal des Maxima-Systems ist Arbeiten mit Listen und Arrays.
Um Listen zu erstellen, verwenden Sie den Befehl makelist. Zum Beispiel mit dem Befehl

Wir haben eine Liste mit dem Namen x erstellt, die aus zehn Elementen besteht, deren Werte gemäß der Formel ermittelt werden.
Um Arrays zu bilden, verwenden Sie den Array-Befehl. Verwenden Sie beispielsweise den Befehl:
![]()
Wir haben ein zweidimensionales Array A gebildet, das aus 10 Zeilen und 5 Spalten besteht. Um das Array mit Elementen zu füllen, verwenden wir eine Schleife mit einem Parameter. Zum Beispiel,
Um Array-Elemente auf dem Bildschirm anzuzeigen, können Sie den folgenden Befehl verwenden:
Ein Array kann ohne vorherige Deklaration gebildet werden. Im folgenden Beispiel haben wir ein eindimensionales Array x gebildet, bestehend aus 5 Elementen, deren Werte mit der Formel x( ich)=Sünde ich

Der Nachteil beim Arbeiten mit Arrays besteht darin, dass die Werte der Array-Elemente in einer Spalte angezeigt werden. Wesentlich komfortabler ist es, wenn die Werte eines (zweidimensionalen) Arrays als Matrix dargestellt werden. Für diese Zwecke können Sie den Befehl genmatrix verwenden. Um beispielsweise ein zweidimensionales Array (Matrix) zu generieren, sollten Sie einen Befehl in der folgenden Form angeben:
Geben wir das resultierende Array aus:

6. Die einfachsten Transformationen von Ausdrücken.
Standardmäßig ist die Autosimplification-Funktion im Maxima-System aktiv, d. h. Das System versucht, den eingegebenen Ausdruck selbst ohne Befehl zu vereinfachen.
Beispiel. Angenommen, Sie müssen den Wert des folgenden numerischen Ausdrucks ermitteln:
Lassen Sie uns den Ausdruck gemäß den Regeln der Maxima-Systemsprache festlegen.

Wie Sie sehen, hat das System mit dem Wert des Ausdrucks geantwortet, obwohl wir keinen Befehl angegeben haben.
Wie kann man das System zwingen, nicht das Ergebnis, sondern den Ausdruck selbst auszugeben? Dazu muss die Vereinfachungsfunktion mit dem Befehl simp:false$ deaktiviert werden. Dann erhalten wir:

Um die Vereinfachungsfunktion zu aktivieren, müssen Sie den Befehl simp:true$ angeben. Die Funktion „Automatische Vereinfachung“ kann sowohl mit numerischen als auch mit einigen nicht numerischen Ausdrücken arbeiten. Zum Beispiel,

Bei der Eingabe können wir mit ihrem Namen auf jede der vorherigen Zellen verweisen und sie in beliebigen Ausdrücken ersetzen. Darüber hinaus wird die letzte Ausgabezelle mit % und die letzte Eingabezelle mit _ bezeichnet. Dadurch können Sie auf das letzte Ergebnis zurückgreifen, ohne durch die Nummer abgelenkt zu werden. Solche Aufrufe von Zellen sollten jedoch nicht missbraucht werden, da es bei der Neuauswertung des gesamten Dokuments oder seiner einzelnen Eingabezellen zu einer Diskrepanz zwischen den Zellennummern kommen kann.
Beispiel. Finden Sie den Wert des Ausdrucks und erhöhen Sie das Ergebnis um das Fünffache.

Es empfiehlt sich, anstelle von Zellnamen Variablen zu verwenden und deren Namen beliebigen Ausdrücken zuzuweisen. In diesem Fall kann jeder mathematische Ausdruck als Wert der Variablen dienen.
Die Werte von Variablennamen bleiben während der gesamten Arbeit mit dem Dokument erhalten. Erinnern wir uns daran, dass, wenn es notwendig ist, die Definition aus einer Variablen zu entfernen, dies mit der Funktion kill(name) erfolgen kann, wobei name der Name des Ausdrucks ist, der zerstört werden soll; darüber hinaus kann es sich dabei entweder um einen von Ihnen vergebenen Namen oder um eine beliebige Eingabe- oder Ausgabezelle handeln. Ebenso können Sie den gesamten Speicher löschen und alle Namen freigeben, indem Sie den Befehl kill(all) eingeben (oder das Menü auswählen). Makhta->Speicher löschen(Klare Erinnerungen)). In diesem Fall werden auch alle I/O-Zellen gelöscht und ihre Nummerierung beginnt wieder bei eins.
Die Funktion „Automatische Vereinfachung“ ist nicht immer in der Lage, einen Ausdruck zu vereinfachen. Darüber hinaus gibt es eine Reihe von Befehlen, die für die Arbeit mit Ausdrücken konzipiert sind: rational und irrational. Schauen wir uns einige davon an.
Ratte (Ausdruck) – wandelt einen rationalen Ausdruck in die kanonische Form um: öffnet alle Klammern, bringt dann alles auf einen gemeinsamen Nenner, summiert und reduziert; wandelt alle Zahlen in endlicher Dezimalschreibweise in rationale Zahlen um. Bei nicht rationalen Transformationen wird die kanonische Form automatisch „aufgehoben“.
ratsimp (Ausdruck) – vereinfacht einen Ausdruck durch rationale Transformationen. Es funktioniert auch „in die Tiefe“, das heißt, die irrationalen Teile des Ausdrucks werden nicht als atomar betrachtet, sondern alle darin enthaltenen rationalen Elemente werden vereinfacht.
fullratsimp(expression) – eine Funktion zur Vereinfachung eines rationalen Ausdrucks durch sequentielles Anwenden der Funktion ratsimp() auf den übergebenen Ausdruck. Aus diesem Grund ist die Funktion etwas langsamer als ratsimp(), liefert aber ein zuverlässigeres Ergebnis.
expand (Ausdruck) – erweitert Klammern in einem Ausdruck auf allen Verschachtelungsebenen. Im Gegensatz zur Funktion ratexpand() werden Brüche nicht auf einen gemeinsamen Nenner reduziert.
radcan(Ausdruck) – eine Funktion zur Vereinfachung von Logarithmus-, Exponential- und Potenzfunktionen mit nicht ganzzahligen rationalen Exponenten, also Wurzeln (Radikalen).
Wenn Sie versuchen, einen Ausdruck in Maxima zu vereinfachen, kann dies oft nur dazu führen, dass er komplexer wird. Eine Erhöhung des Ergebnisses kann dadurch auftreten, dass nicht bekannt ist, welche Werte die im Ausdruck enthaltenen Variablen annehmen können. Um dies zu vermeiden, sollten Sie die Werte, die eine Variable annehmen kann, einschränken. Dies geschieht mit der Funktion „Annahme(Bedingung)“. Daher kann in manchen Fällen das beste Ergebnis durch die Kombination von radcan() mit ratsimp() oder fullratsimp() erzielt werden.