RSA-Verschlüsselungsalgorithmus. Beispiel für den RSA-Verschlüsselungsalgorithmus Technologie zur Implementierung des RSA-Algorithmus

Einleitung 3

Hauptteil 5

1Schöpfungsgeschichte 5

2Beschreibung des Algorithmus 5

2.1Schlüssel erstellen 6

2.2 Verschlüsselung und Entschlüsselung 6

2.3Verwenden Sie Beispiel 7

Fazit 9

Liste der verwendeten Quellen 10

Einführung

Kryptographie ist ein spezielles System zur Änderung gewöhnlicher Schrift, das dazu dient, Texte nur für eine begrenzte Anzahl von Personen verständlich zu machen, die dieses System kennen.

Kryptographie ist die Wissenschaft vom Schutz von Informationen mithilfe mathematischer Methoden.

Moderne Kryptographie umfasst:

symmetrische Kryptosysteme;

asymmetrische Kryptosysteme;

elektronische digitale Signatursysteme (EDS);

Hash-Funktionen;

Schlüsselverwaltung;

Erhalten versteckter Informationen;

Quantenkryptographie.

Symmetrische Verschlüsselung – symmetrische Algorithmen sind solche, bei denen derselbe geheime Schlüssel (der nur dem Absender und dem Empfänger bekannt ist) für die Verschlüsselung und Entschlüsselung verwendet wird.

Gängige symmetrische Verschlüsselungsalgorithmen:

AES (Advanced Encryption Standard) – amerikanischer Verschlüsselungsstandard;

GOST 28147-89 – inländischer Datenverschlüsselungsstandard;

DES (Data Encryption Standard) – Datenverschlüsselungsstandard in den USA bis AES;

3DES (Triple-DES, Triple-DES);

IDEA (Internationaler Datenverschlüsselungsalgorithmus);

SEED – Koreanischer Datenverschlüsselungsstandard;

Camellia ist eine für die Verwendung in Japan zertifizierte Chiffre;

XTEA ist der am einfachsten zu implementierende Algorithmus.

Asymmetrische Kryptoalgorithmen sollen in erster Linie den Hauptnachteil symmetrischer Kryptosysteme beseitigen – die Komplexität der Verwaltung und Verteilung von Schlüsseln.

Die Grundlage aller asymmetrischen kryptografischen Algorithmen ist die hohe Rechenkomplexität der Wiederherstellung von Klartext ohne Kenntnis des privaten Schlüssels.

Beispiele für asymmetrische Kryptoalgorithmen:

Diffie-Hellmann;

RSA – Rivest, Shamir, Adelman – basiert auf der Komplexität des Problems der Faktorisierung großer Zahlen in kurzer Zeit;

DSA – Digitaler Signaturalgorithmus, US-Standard;

GOST R 34.10 – 94, 2001, Standards der Russischen Föderation.

In dieser Zusammenfassung werden wir den asymmetrischen kryptografischen Verschlüsselungsalgorithmus – den RSA-Algorithmus – im Detail betrachten.

Hauptteil

Der RSA-Algorithmus (ein Akronym für Rivest, Shamir und Adleman) ist ein kryptografischer Algorithmus mit öffentlichem Schlüssel, der sich die rechnerische Komplexität des Problems der Faktorisierung großer Ganzzahlen zunutze macht. Das RSA-Kryptosystem war das erste System, das sowohl für die Verschlüsselung als auch für die digitale Signatur geeignet war.

Geschichte der Schöpfung

Der im November 1976 veröffentlichte Artikel „New Directions in Cryptography“ von Whitfield Diffie und Martin Hellman revolutionierte das Verständnis kryptografischer Systeme, indem er den Grundstein für die Public-Key-Kryptografie legte. Der anschließend entwickelte Diffie-Hellman-Algorithmus ermöglichte es zwei Parteien, über einen unsicheren Kommunikationskanal an einen gemeinsamen geheimen Schlüssel zu gelangen. Dieser Algorithmus löste jedoch das Authentifizierungsproblem nicht. Ohne zusätzliche Tools könnten Benutzer nicht sicher sein, mit wem sie den gemeinsamen geheimen Schlüssel generiert haben.

Nach dem Studium dieses Artikels begannen die drei Wissenschaftler Ronald Linn Rivest, Adi Shamir und Leonard Adleman vom Massachusetts Institute of Technology (MIT) mit der Suche nach einer mathematischen Funktion, die die Implementierung eines von Whitfield Diffie und Martin Hellman formulierten Modells eines kryptografischen Systems mit öffentlichem Schlüssel ermöglichen würde . Nachdem sie mehr als 40 Möglichkeiten durchgearbeitet hatten, entwickelten sie einen Algorithmus, der auf dem Unterschied zwischen der Leichtigkeit, große Primzahlen zu finden, und der Schwierigkeit, das Produkt zweier großer Primzahlen zu faktorisieren, basiert und den sie später RSA nannten. Das System wurde nach den Anfangsbuchstaben der Nachnamen seiner Erfinder benannt.

Beschreibung des Algorithmus

Der erste Schritt in jedem asymmetrischen Algorithmus besteht darin, ein Schlüsselpaar – einen öffentlichen und einen privaten – zu erstellen und den öffentlichen Schlüssel „in der ganzen Welt“ zu verteilen.

Schlüssel erstellen

Für den RSA-Algorithmus besteht die Phase der Schlüsselerstellung aus den folgenden Vorgängen:

Die Zahl wird als offener Exponent bezeichnet

Verschlüsselung und Entschlüsselung

Nehmen wir an, der Absender möchte dem Empfänger eine Nachricht senden.

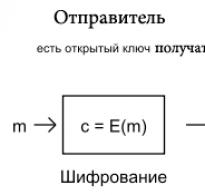
Nachrichten sind ganze Zahlen im Bereich von 0 bis , d. h. . Abbildung 1 zeigt ein Diagramm des RSA-Algorithmus.

Abbildung 1 – Diagramm des RSA-Algorithmus

Absender-Algorithmus:

Empfängeralgorithmus:

Die Gleichungen (1) und (2), auf denen das RSA-Schema basiert, bestimmen die zueinander inversen Transformationen der Menge.

Anwendungsbeispiel

Tabelle 1 zeigt ein Beispiel für die Verwendung des RSA-Algorithmus. Der Absender schickte eine verschlüsselte Nachricht „111111“ und der Empfänger entschlüsselte sie mit seinem privaten Schlüssel.

Tabelle 1 – Schrittweise Ausführung des RSA-Algorithmus

Abschluss

In dieser Zusammenfassung wurde der asymmetrische Verschlüsselungsalgorithmus RSA ausführlich besprochen. Die Entstehungsgeschichte wurde beschrieben, Algorithmen zur Schlüsselerstellung, Verschlüsselung und Entschlüsselung wurden beschrieben. Außerdem wird ein Beispiel für den praktischen Einsatz des RSA-Algorithmus vorgestellt.

Liste der verwendeten Quellen

Semenov Yu.A. Internetprotokolle // M.: Prospekt, 2011. – 114 S.

Belyaev A.V. Methoden und Mittel der Informationssicherheit // Black Branch der Staatlichen Technischen Universität St. Petersburg, 2010. – 142 S.

Venbo M. Moderne Kryptographie. Theorie und Praxis // M.: Williams, 2005. - 768 S.

Schneier B. Angewandte Kryptographie. Protokolle, Algorithmen, Quelltexte // M.: Triumph, 2002. - 816 S.

RSA-Algorithmus // Internetressource: http://ru.wikipedia.org/wiki/Rsa

Im zweiten Teil betrachten wir den beliebten RSA-Algorithmus, bei dem ein öffentlicher Schlüssel zur Verschlüsselung verwendet wird. Aber zuerst möchte ich Sie noch einmal warnen. Der in diesem Artikel vorgestellte Code dient nur zu Bildungszwecken. Kryptographie ist ein sehr weites und komplexes Gebiet, und um Probleme zu vermeiden, empfehle ich, Informationen nicht mit meinem Hack zu verschlüsseln.

Im zweiten Teil betrachten wir den beliebten RSA-Algorithmus, bei dem ein öffentlicher Schlüssel zur Verschlüsselung verwendet wird. Aber zuerst möchte ich Sie noch einmal warnen. Der in diesem Artikel vorgestellte Code dient nur zu Bildungszwecken. Kryptographie ist ein sehr weites und komplexes Gebiet, und um Probleme zu vermeiden, empfehle ich, Informationen nicht mit meinem Hack zu verschlüsseln.

RSA-Algorithmus

Verschlüsselung mit einem öffentlichen Schlüssel

Die Verschlüsselung mit öffentlichen Schlüsseln wird überall verwendet. Wenn Sie mindestens einmal online etwas bezahlt haben, haben Sie diese Methode bereits verwendet (hoffe ich!). Es stellt sich sofort die Frage, wie dieser Schutz funktioniert. Wenn ich meine Kreditkartennummer eingebe, um etwas zu kaufen, warum kann dann niemand außer dem Empfänger diese Informationen sehen? Lassen Sie mich Ihnen eine Metapher geben. Um einen Tresor zu öffnen, benötigen Sie einen Schlüssel (oder einen Hammer, aber zum Glück sind Tresore und Schlösser gegen solche Einwirkungen resistent). Bei der Public-Key-Verschlüsselung passiert fast das Gleiche. Sie zeigen das Schloss für jeden sichtbar, aber nur wenige haben den Schlüssel zu diesem Schloss, und es ist fast unmöglich, die Tür mit anderen Methoden zu öffnen.

RSA ist einer der Algorithmen, der das obige Schema implementiert. Darüber hinaus können wir diesen Algorithmus verwenden, um die Authentizität unserer Identität zu überprüfen. Wenn Sie eine verschlüsselte Nachricht mit einem privaten Schlüssel an jemanden senden, kann der Empfänger Ihre Nachricht mit dem öffentlichen Schlüssel entschlüsseln. Mit dieser Technologie können Nachrichten signiert und so die Authentizität des Absenders bestätigt werden.

Demoprogramm basierend auf dem RSA-Algorithmus

Abhängig von der Struktur der verwendeten Schlüssel werden Verschlüsselungsverfahren unterteilt in:

• symmetrisch: Außenstehende kennen vielleicht den Verschlüsselungsalgorithmus, aber ein kleiner Teil der geheimen Informationen ist unbekannt – der Schlüssel, der für Absender und Empfänger der Nachricht gleich ist; Beispiele: DES, 3DES, AES, Blowfish, Twofish, GOST 28147-89
• Asymmetrische Verschlüsselung: Außenstehende kennen möglicherweise den Verschlüsselungsalgorithmus und möglicherweise den öffentlichen Schlüssel, nicht jedoch den privaten Schlüssel, der nur dem Empfänger bekannt ist. Kryptografische Systeme mit öffentlichem Schlüssel werden derzeit häufig in verschiedenen Netzwerkprotokollen verwendet, insbesondere in den TLS-Protokollen und seinem Vorgänger SSL (zugrunde liegendes HTTPS) sowie SSH, PGP, S/MIME usw. Der russische Standard verwendet asymmetrische Verschlüsselung – .

Derzeit wird die asymmetrische Public-Key-Verschlüsselung RSA (steht für Rivest, Shamir und Aldeman – die Erfinder des Algorithmus) von den meisten Produkten auf dem Informationssicherheitsmarkt verwendet.

Seine kryptografische Stärke beruht auf der Schwierigkeit, große Zahlen zu faktorisieren, nämlich auf der außergewöhnlichen Schwierigkeit der Aufgabe, einen geheimen Schlüssel auf der Grundlage eines öffentlichen Schlüssels zu bestimmen, da dies die Lösung des Problems der Existenz von Teilern einer ganzen Zahl erfordern würde. Die sichersten Systeme verwenden 1024-Bit- und größere Zahlen.

Schauen wir uns den RSA-Algorithmus aus praktischer Sicht an.

Zuerst müssen Sie öffentliche und private Schlüssel generieren:

• Nehmen wir zwei große Primzahlen p und q.
• Definieren wir n als das Ergebnis der Multiplikation von p mit q (n= p*q).
• Wählen wir eine Zufallszahl, die wir d nennen. Diese Zahl muss mit dem Ergebnis der Multiplikation (p-1)*(q-1) relativ teilerfremd sein (keinen gemeinsamen Teiler außer 1 haben).
• Definieren wir eine Zahl e, für die die folgende Beziehung (e*d) mod ((p-1)*(q-1))=1 gilt.
• Nennen wir den öffentlichen Schlüssel die Zahlen e und n und den geheimen Schlüssel die Zahlen d und n.

Um Daten mit einem öffentlichen Schlüssel (e,n) zu verschlüsseln, benötigen Sie Folgendes:

• Teilen Sie den verschlüsselten Text in Blöcke auf, von denen jeder als Zahl M(i)=0,1,2..., n-1 (also nur bis n-1) dargestellt werden kann.
• Verschlüsseln Sie den Text, der als Folge von Zahlen M(i) betrachtet wird, mit der Formel C(i)=(M(I)^e)mod n.

Um diese Daten mit dem geheimen Schlüssel (d,n) zu entschlüsseln, müssen die folgenden Berechnungen durchgeführt werden: M(i) = (C(i)^d) mod n. Als Ergebnis wird eine Menge von Zahlen M(i) erhalten, die den Originaltext darstellen.

Das folgende Beispiel veranschaulicht den RSA-Verschlüsselungsalgorithmus anschaulich:

Lassen Sie uns die „CAB“-Nachricht mit dem RSA-Algorithmus verschlüsseln und entschlüsseln. Nehmen wir der Einfachheit halber kleine Zahlen – das verkürzt unsere Berechnungen.

• Wählen wir p=3 und q=11.
• Definieren wir n= 3*11=33.
• Finden wir (p-1)*(q-1)=20. Daher ist d beispielsweise gleich 3: (d=3).
• Wählen wir die Zahl e mit der folgenden Formel: (e*3) mod 20=1. Das bedeutet, dass e beispielsweise gleich 7 ist: (e=7).
• Stellen wir uns die verschlüsselte Nachricht als eine Zahlenfolge im Bereich von 0 bis 32 vor (denken Sie daran, dass sie mit n-1 endet). Buchstabe A =1, B=2, C=3.

Verschlüsseln wir nun die Nachricht mit dem öffentlichen Schlüssel (7.33).

C1 = (3^7) mod 33 = 2187 mod 33 = 9;
C2 = (1^7) mod 33 = 1 mod 33 = 1;
C3 = (2^7) mod 33 = 128 mod 33 = 29;

Nun entschlüsseln wir die Daten mit dem privaten Schlüssel (3.33).

M1=(9^3) mod 33 =729 mod 33 = 3(C);
M2=(1^3) mod 33 =1 mod 33 = 1(A);
M3=(29^3) mod 33 = 24389 mod 33 = 2(B);

Daten entschlüsselt!

Endlich ist es an der Zeit, mit der Beschreibung des RSA-Kryptosystems zu beginnen. Wir müssen nicht nur erklären, wie es funktioniert, sondern auch seine Sicherheit im Detail besprechen; Mit anderen Worten: Warum ist es so schwierig, eine mit dem RSA-Kryptosystem verschlüsselte Nachricht zu knacken?

§ 12.1. Über den Anfang und das Ende

Um ein Einzelbenutzer-RSA-Verschlüsselungssystem zu implementieren, müssen Sie zwei verschiedene Primzahlen p und q auswählen und deren Produkt berechnen. Die Primzahlen p und q werden geheim gehalten, während die Zahl Teil des öffentlichen Schlüssels wird. In § 12.5 besprechen wir ausführlich die Methode zur Auswahl wichtiger Primzahlen und wie sich diese Auswahl auf die Zuverlässigkeit des Systems auswirkt.

Eine Nachricht (die als Ganzzahl betrachtet werden kann) wird durch Potenzierung modulo verschlüsselt. Daher müssen wir zunächst einen Weg finden, den Text der Nachricht als Liste von Modulo-Klassen darzustellen den Verschlüsselungsprozess, bereitet aber lediglich die Nachricht so vor, dass sie verschlüsselt werden kann.

Nehmen wir der Einfachheit halber an, dass der Nachrichtentext nur Wörter enthält, die in Großbuchstaben geschrieben sind. Die Nachricht ist also letztlich eine Folge von Buchstaben und Leerzeichen. Der erste Schritt besteht darin, jeden Buchstaben der Nachricht durch eine Zahl zu ersetzen, die aus der folgenden Tabelle ausgewählt wird:

(siehe Scan)

Das Leerzeichen zwischen den Wörtern wird durch die Zahl 99 ersetzt. Nachdem wir diesen Vorgang durchgeführt haben, erhalten wir eine Zahl, die möglicherweise sehr groß ist, wenn die Nachricht lang ist. Dies ist jedoch nicht die endgültige Zahl, die wir anstreben, sondern nur eine Reihe von Modulo-Klassen. Und jetzt müssen wir die numerische Darstellung der Nachricht in Teile zerlegen, von denen jedes eine natürliche Zahl ist, die diese Teile normalerweise nicht überschreitet Nachrichtenblöcke.

Die numerische Darstellung des Mottos „Erkenne dich selbst“ sieht beispielsweise so aus:

Durch die Auswahl einfacher erhalten wir das Produkt. Daher muss die numerische Darstellung der oben geschriebenen Nachricht in Blöcke unterteilt werden, die kleiner als 23.393 sind.

Natürlich ist die Auswahl der Blöcke nicht eindeutig, aber auch nicht völlig willkürlich. Beispielsweise um Unklarheiten auf der Bühne zu vermeiden

Bei der Entschlüsselung sollten keine Blöcke hervorgehoben werden, die mit Null beginnen.

Beim Entschlüsseln einer mit dem RSA-Verschlüsselungssystem verschlüsselten Nachricht wird eine Folge von Blöcken erhalten. Anschließend werden sie miteinander verbunden, um eine numerische Darstellung der Nachricht zu erzeugen. Und erst nach dem Ersetzen der Zahlen durch Buchstaben gemäß der obigen Tabelle ist es möglich, die ursprüngliche Nachricht zu lesen.

Bitte beachten Sie, dass jeder Buchstabe in der Tabelle mit einer zweistelligen Zahl kodiert ist. Dies geschieht, um Verwirrung zu vermeiden. Angenommen, wir nummerieren die Buchstaben der Reihe nach, beginnend mit 1, d. h. A entspricht 1, B entspricht 2 und so weiter. In diesem Fall können wir nicht sicher sagen, ob Block 12 ein Buchstabenpaar oder nur einen Buchstaben, den zwölften Buchstaben des Alphabets, darstellt. Natürlich können Sie für die numerische Darstellung einer Nachricht jede Eins-zu-eins-Entsprechung zwischen Buchstaben und Zahlen verwenden, zum Beispiel die -Kodierung, bei der die Übersetzung der Nachricht in digitale Form automatisch von einem Computer durchgeführt wird.

§ 12.2. Verschlüsselung und Entschlüsselung

Eine mit der Methode von § 12.1 für die Verschlüsselung vorbereitete Nachricht besteht aus einer Folge von Blöcken, von denen jeder eine Zahl kleiner als ist. Lassen Sie uns nun diskutieren, wie jeder Block verschlüsselt wird. Dazu benötigen wir eine Zahl, die dem Produkt aus Primzahlen und einer natürlichen Zahl entspricht, modulo invertierbar, d. h. Zahl, die die Bedingung erfüllt

Erinnern wir uns daran, dass die Zahl aus bekannten p und q leicht berechnet werden kann. Wirklich,

Das Paar wird als öffentlicher oder Verschlüsselungsschlüssel des von uns beschriebenen RSA-Kryptosystems bezeichnet. Der Nachrichtenblock sei eine Ganzzahl, die die Ungleichung erfüllt. Wir verwenden das Symbol, um den Block der verschlüsselten Nachricht zu bezeichnen, der gemäß der folgenden Regel berechnet wird:

Beachten Sie, dass jeder Nachrichtenblock separat verschlüsselt wird. Daher besteht eine verschlüsselte Nachricht tatsächlich aus separaten verschlüsselten Blöcken. Darüber hinaus können wir diese Blöcke nicht zu einer großen Zahl zusammenfassen, da dies die Entschlüsselung der Nachricht unmöglich machen würde. Den Grund dafür werden wir bald sehen.

Kehren wir zu dem Beispiel zurück, das wir im ersten Absatz betrachtet haben. Wir haben Folgendes festgelegt: Jetzt müssen wir eine Zahl auswählen. Denken Sie daran, dass sie teilerfremd sein muss mit Die kleinste Primzahl, die 23088 nicht teilt, ist gleich 5. Stellen wir ein, um den ersten Block der Nachricht aus § 12.1 zu codieren um die Subtraktion der Zahl 25245 modulo 23393 zu bestimmen. Mit einem symbolischen Berechnungsprogramm (oder einem Taschenrechner, wenn Sie Geduld haben) erhalten wir, dass die erforderliche Subtraktion 22.752 beträgt. Die verschlüsselte Nachricht wird also durch die folgende Blockfolge dargestellt :

Sehen wir uns an, wie Blöcke einer verschlüsselten Nachricht dekodiert werden. Um mit der Entschlüsselung zu beginnen, müssen wir das inverse Element zu Modulo kennen. Das letzte davon ist eine natürliche Zahl, die wir mit bezeichnen. Das Paar wird als Geheimnis oder Dekodierungsschlüssel des RSA-Verschlüsselungssystems bezeichnet. Wenn a ein Block einer verschlüsselten Nachricht ist, dann die entsprechende Entschlüsselung

Das Ergebnis der Operation ist:

Bevor wir zum Beispiel zurückkehren, sind einige Kommentare erforderlich. Erstens ist die Berechnung sehr einfach, wenn Sie wissen, dass der geheime Schlüssel tatsächlich mithilfe des erweiterten euklidischen Algorithmus ermittelt wird. Zweitens: Wenn es sich bei dem Block um die Originalnachricht handelt, können wir mit Recht Gleichheit erwarten. Mit anderen Worten: Wenn wir einen Block einer verschlüsselten Nachricht dekodieren, hoffen wir, den entsprechenden Block der Originalnachricht herauszufinden. Dass dies der Fall sein wird, ergibt sich nicht direkt aus dem oben beschriebenen Algorithmus, wir werden jedoch im nächsten Absatz alles im Detail besprechen.

Wie wir in der Einleitung und im gesamten Buch dargelegt haben, muss man ein RSA-Kryptosystem schließlich faktorisieren, weil man wissen muss, wie man die Nachricht entschlüsselt. Sobald die Funktionsweise des Systems jedoch im Detail beschrieben wird, ist klar Letztere Aussage ist nicht ganz korrekt. Um die Verschlüsselung zu lesen, müssen Sie zusätzlich zum Element selbst nur die Modulo-Inverse des Elements kennen. Um das System zu hacken, reicht es daher aus, mit bekannten Zahlen zu rechnen. Es stellt sich heraus, dass diese Berechnung dem Faktorisieren einer Zahl entspricht , wie wir in § 12.4 sehen werden.

Im besprochenen Beispiel wenden wir den erweiterten euklidischen Algorithmus an, um die Zahlen und 5 zu bestimmen.

(siehe Scan)

Daher wäre die Umkehrung von 5 Modulo -9235 und

Die kleinste natürliche Zahl, vergleichbar mit -9235 Modulo. Um einen Block einer verschlüsselten Nachricht zu dekodieren, müssen wir ihn auf die Potenz von 13.853 Modulo 23.393 erhöhen. In unserem Beispiel ist der erste kodierte Block 22.752 75213853 modulo 23.393 erhalten wir. Beachten Sie, dass selbst bei solch kleinen Zahlen die Anforderungen für den Betrieb des RSA-Kryptosystems die Fähigkeiten der meisten Taschenrechner übersteigen.

§ 12.3. Warum funktioniert es?

Wie bereits erwähnt, führen die oben beschriebenen Schritte nur dann zu einem funktionierenden Kryptosystem, wenn durch die Dekodierung jedes Blocks der verschlüsselten Nachricht der entsprechende Block des Originals wiederhergestellt wird. Nehmen wir an, dass wir es mit einem RSA-System zu tun haben, das einen öffentlichen und einen privaten Schlüssel hat. Unter Verwendung der Notation von § 12.2 müssen wir zeigen, dass für jede ganze Zahl, die die Ungleichung erfüllt, die Identität gilt

Tatsächlich reicht es aus, das zu beweisen

Tatsächlich sind sowohl 6 als auch nichtnegative ganze Zahlen kleiner. Daher sind sie genau dann im absoluten Wert vergleichbar, wenn sie gleich sind. Dies erklärt insbesondere, warum wir die numerische Darstellung der Nachricht in kleinere Blöcke aufteilen. Darüber hinaus ist daraus ersichtlich, dass Blöcke vorhanden sind

Die verschlüsselte Nachricht muss separat aufgeschrieben werden, sonst funktioniert unsere Argumentation nicht.

Aus den Verschlüsselungs- und Entschlüsselungsrezepten folgt dies

Da die Elemente im Modul zueinander invers sind, gibt es ein natürliches k, sodass die Zahlen aufgrund der Bedingung größer sind. Daher erhalten wir durch Einsetzen anstelle des Produkts in Gleichung (3.1).

Lassen Sie uns nun den Satz von Euler verwenden, der besagt, dass Daher, d. h.

und wir hätten den Beweis vollständig erhalten, wenn sich darin nicht ein kleiner Fehler eingeschlichen hätte.

Wenn Sie unsere Argumentation noch einmal sorgfältig prüfen, werden Sie feststellen, dass wir die Bedingungen des Satzes von Euler nicht berücksichtigt haben. Tatsächlich muss vor der Anwendung des Theorems sichergestellt werden, dass die Zahlen zueinander prim sind. Dies muss anscheinend bei der Vorbereitung einer Nachricht für die Verschlüsselung überwacht werden, d. h. Wenn Sie die numerische Darstellung einer Nachricht in Blöcke unterteilen, müssen Sie sicherstellen, dass alle resultierenden Blöcke teilerfremd sind. Glücklicherweise ist dies nicht notwendig, da der Vergleich tatsächlich für jeden Block durchgeführt wird. Und der Fehler liegt nicht im Ergebnis, das wir beweisen wollen, sondern nur im Beweis selbst. Der richtige Ansatz basiert auf der Argumentation, die im Beweis des Corcelt-Theorems in Kapitel 7 verwendet wurde.

Denken Sie daran, dass es verschiedene Primzahlen gibt. Definieren wir die Reste einer Zahl modulo Since

Die Berechnungen für beide Primzahlen sind ähnlich, wir werden den Fall nur im Detail ausarbeiten. Das haben wir also bereits gesehen

für eine ganze Zahl Deshalb,

Wir möchten nun den Satz von Fermat anwenden, haben aber nur dann das Recht, dies zu tun, wenn er nicht dividiert. Lassen Sie diese Anforderung erfüllt sein. Dann verstehen wir das

Indem wir den Satz von Fermat durch den Satz von Euler ersetzten, haben wir das aufgetretene Problem nicht gelöst: Der Vergleich ist nur für einige, aber nicht für alle Blöcke gültig. Nun müssen jedoch die Blöcke, für die die Argumentation nicht funktioniert, durch geteilt werden. Wenn es sich teilt, dann sind beide 6 und im Modul mit 0 vergleichbar und daher miteinander vergleichbar. Somit ist der nachgewiesene Vergleich auch in diesem Fall gültig. Daher gilt der Vergleich für jede Ganzzahl. Beachten Sie, dass dies nicht der Fall ist. hätte bei der Anwendung des Eulerschen Theorems auf eine ähnliche Argumentation zurückgreifen können. In der Tat bedeutet Ungleichheit keinen Vergleich, da die Zahl zusammengesetzt ist.

Wir haben also bewiesen, dass der Vergleich gleichermaßen bewiesen ist. Mit anderen Worten: Dividiert durch und Aber sind unterschiedliche Primzahlen, sodass uns das Lemma aus § 3.6 garantiert, dass A geteilt wird, da wir für jede ganze Zahl haben. Mit anderen Worten: As Wie wir am Anfang des Absatzes bemerkt haben, reicht dies aus, um die Gleichheit zu beweisen, da beide Teile nicht negative ganze Zahlen kleiner als sind. Zusammenfassend können wir das sagen

Der Algorithmus des vorherigen Absatzes führt zu einem praktischen Kryptosystem. Jetzt müssen Sie sicherstellen, dass es zuverlässig ist.

§ 12.4. Warum ist das System zuverlässig?

Denken Sie daran, dass RSA ein Verschlüsselungssystem mit einem öffentlichen Schlüssel ist, der aus dem Produkt verschiedener Primzahlen und einer modulo-invertierbaren natürlichen Zahl besteht. Schauen wir uns genau an, was getan werden kann, um RSA zu knacken, wenn nur ein Paar bekannt ist

Um einen mit RSA verschlüsselten Block zu dekodieren, müssen wir die Umkehrung von Modulo k kennen. Das Problem besteht darin, dass praktisch die einzige bekannte Möglichkeit, dies zu tun, auf der Anwendung des erweiterten euklidischen Algorithmus basiert. Um jedoch mit der Formel aus § 9.4 zu berechnen, Wir müssen wissen, was die ursprüngliche Aussage bestätigt: Das Brechen von RSA erfordert Faktorisierung. Und da die Zersetzungsschwierigkeiten grundlegend sind, ist das RSA-System sicher.

Man kann natürlich davon ausgehen, dass eines Tages jemand einen Algorithmus entdecken wird, der ohne Informationen über die Faktoren einer Zahl berechnet. Was zum Beispiel passieren wird, wenn jemand eine effektive Möglichkeit findet, direkt durch zu bestimmen. Tatsächlich ist dies gerechtfertigt eine getarnte Methode der Expansion Genauer gesagt, wenn

bekannt sind, können wir tatsächlich leicht berechnen:

Daher ist die Summe der erforderlichen Primteiler bekannt. Weiter,

daher ist auch der Unterschied bekannt. Durch die Lösung eines einfachen Systems linearer Gleichungen können wir nun leicht eine Faktorisierung finden.

Das bedeutet, dass der Algorithmus, der die Zahl berechnet, die Zahl tatsächlich in Faktoren zerlegt, es handelt sich also um einen Vogel von einer Feder. Aber es ist zu früh, um sich zu beruhigen. Sie können in Ihren Fantasien noch weiter gehen und annehmen, dass jemand einen Algorithmus erfunden hat, der direkt durch bestimmt. Wenn wir also wissen, dann kennen wir die Zahl, die ein Vielfaches davon ist. Es stellt sich heraus, dass solche Informationen auch für die Zerlegung ausreichen. Ein probabilistischer Algorithmus, der zu einer solchen Zerlegung führt, kann in V gefunden werden. Übung 7 zeigt einen ähnlichen (aber einfacheren) Zerlegungsalgorithmus unter der Annahme, dass das Rabin-Kryptosystem gebrochen werden kann. Es gibt Ihnen eine Vorstellung vom probabilistischen Algorithmus von .

Es bleibt die letzte Möglichkeit zum Hacken: Der Versuch, den Block direkt durch Modulo-Rest wiederherzustellen. Wenn er groß genug ist, ist eine systematische Suche aller möglichen Kandidaten für die Suche der einzige Ausweg. Noch ist niemandem etwas Besseres eingefallen. Wir haben die Hauptargumente aufgelistet, die erklären, warum der Bruch des RSA-Kryptosystems als gleichbedeutend mit einer Faktorisierung angesehen wird, obwohl es noch keinen schlüssigen Beweis für diese Aussage gibt.

§ 12.5. Einfache auswählen

Aus der vorherigen Diskussion geht hervor, dass es für die Sicherheit des RSA-Kryptosystems wichtig ist, die richtigen Primzahlen zu wählen. Wenn diese klein sind, kann das System natürlich leicht gehackt werden. Es reicht jedoch nicht aus, große Werte zu wählen. Selbst wenn p und q zwar groß, der Unterschied aber gering ist, kann ihr Produkt mit dem Fermat-Algorithmus leicht faktorisiert werden (siehe § 3.4).

Das ist kein leeres Gerede. Im Jahr 1995 knackten zwei Studenten einer amerikanischen Universität eine öffentliche Version von RSA. Dies wurde aufgrund der schlechten Auswahl der Primfaktoren des Systems möglich.

Andererseits wird RSA schon seit langem verwendet und bei sorgfältiger Auswahl der Primfaktoren erweist sich das System tatsächlich als recht zuverlässig. Daher benötigt jeder RSA-Verschlüsselungsprogrammierer eine effektive Methode zur erfolgreichen Auswahl von Primzahlen.

Angenommen, wir möchten ein RSA-Kryptosystem mit einem öffentlichen Schlüssel erstellen, in dem die ganze Zahl etwa Ziffern hat. Wählen wir zunächst eine Primzahl aus, deren Anzahl an Zeichen in der Nähe liegt. Derzeit beträgt die empfohlene Schlüsselgröße für den persönlichen Gebrauch 768 Bit, d. h. sollte etwa 231 Ziffern lang sein. Um eine solche Zahl zu konstruieren, benötigen wir zwei einfache Zahlen mit beispielsweise 104 und 127 Ziffern. Bitte beachten Sie, dass die so gewählten Primzahlen recht weit voneinander entfernt sind, d. h. Die Verwendung des Fermat-Algorithmus zur Zerlegung ist in dieser Situation unpraktisch. Darüber hinaus müssen wir sicherstellen, dass bei der Faktorisierung von Zahlen in Primfaktoren nicht nur kleine, sondern auch große Faktoren beteiligt sind. Andernfalls wird die Zahl tatsächlich zu einer leichten Beute für einige bekannte Zerlegungsalgorithmen (siehe). Betrachten wir nun eine Methode, mit der Primzahlen gefunden werden, die die aufgeführten Bedingungen erfüllen.

Zunächst benötigen wir ein einfaches Ergebnis über die Verteilung von Primzahlen. Erinnern wir uns daran, was die Anzahl der Primzahlen bezeichnet, die x nicht überschreitet. Angesichts des Primzahlsatzes sehen wir, dass die Zahl für große x ungefähr gleich dem natürlichen Logarithmus ist

auf der Grundlage (siehe § 4.5). Lassen Sie es eine sehr große, etwas positive Zahl sein. Wir wollen die Anzahl der dazwischen liegenden Primzahlen abschätzen und die Differenz abschätzen. Dank des Primzahlsatzes und der Eigenschaften des Logarithmus ist die Differenz ungefähr gleich

Unter der Annahme, dass es sehr klein ist, können wir davon ausgehen, dass der Wert gleich 0 ist, und eine vernünftige Schätzung der Differenz erhalten. Die Anzahl der eingeschlossenen Primzahlen ist also natürlich ungefähr gleich, je größer x ist Für eine detailliertere Einführung in eine solche Schätzung siehe ([D. 10]).

Angenommen, wir müssen eine Primzahl in der Umgebung einer ganzen Zahl x wählen. Aus Gründen der Eindeutigkeit gehen wir davon aus, dass x von der Ordnung ist, und suchen nach einer Primzahl im Intervall von x bis. Es wäre nützlich, im Voraus zu wissen, wie viele Primzahlen in diesem Intervall liegen. Um die Anzahl der Primzahlen abzuschätzen, können Sie das soeben erhaltene Ergebnis verwenden. In unserem Beispiel liegt der Wert in einer sehr kleinen Größenordnung: Daher schließen wir anhand der oben geschriebenen Formel, dass der Abstand zwischen ungefähr liegt

Primzahlen. Am Ende des zweiten Absatzes von Kapitel 11 haben wir eine Strategie zum Beweis der Primzahl einer gegebenen ungeraden Zahl formuliert. Sie besteht aus drei Schritten.

Das Rivest-Shamir-Adleman (RSA)-Schema ist derzeit das einzige allgemein akzeptierte und praktisch verwendete Verschlüsselungsschema mit öffentlichem Schlüssel.

Das RSA-Schema ist eine Blockverschlüsselung, bei der sowohl der Klartext als auch der Chiffretext durch ganze Zahlen im Bereich von 0 bis dargestellt werden P- 1 für einige P.

Der Klartext wird in Blöcken verschlüsselt, von denen jeder einen Binärwert enthält, der kleiner als eine bestimmte Zahl ist P. Das bedeutet, dass die Blocklänge nicht mehr als log2(“) betragen sollte. In der Praxis wird die Blocklänge so gewählt 2 k Bits wo 2 zu Das von Rivest, Shamir und Adleman entwickelte Schema basiert auf Ausdrücken mit Kräften. Die Verschlüsselung und Entschlüsselung für den Klartextblock M und den Chiffretextblock C kann durch die folgenden Formeln dargestellt werden:

Sowohl der Absender als auch der Empfänger müssen die Bedeutung kennen P. Der Absender kennt die Bedeutung e, und nur der Empfänger kennt den Wert D. Somit ist dieses Schema ein Verschlüsselungsalgorithmus mit öffentlichem Schlüssel KU= (e, p), und privater Schlüssel KR = (d, p).

Damit dieser Algorithmus für die Public-Key-Verschlüsselung verwendet werden kann, müssen folgende Voraussetzungen erfüllt sein:

Es muss solche Werte geben e, d Und P, Was M ed = M(mod P) für alle M p.

IVT und sollte relativ einfach zu berechnen sein C c1 für alle Werte von M p.

Es muss fast unmöglich sein, es zu bestimmen D je nach Verfügbarkeit ihr p.

Lassen Sie uns zunächst die erste Anforderung analysieren und uns später den Rest ansehen. Es ist notwendig, eine Beziehung der Form zu finden

Hier ist die Folgerung aus dem Satz von Euler am besten geeignet: für zwei beliebige solcher Primzahlen R Und Q und zwei beliebige solcher ganzen Zahlen Pete, Was n=pqn0 und eine beliebige ganze Zahl Zu Es gelten folgende Beziehungen:

wobei φ(i) die Euler-Funktion ist, deren Wert gleich der Anzahl der positiven ganzen Zahlen kleiner als ist P und koprimieren mit P.

Im Falle von einfach R Und Q wir haben f (pq) - (S - 1 )(Q - 1). Daher wird das erforderliche Verhältnis unter der Bedingung erhalten

Dies entspricht den folgenden Beziehungen:

diese. ihr d sind zueinander invers modulo φ(i). Beachten Sie, dass dies nach den Regeln der Arithmetik in Residuenklassen nur dann erfolgen kann, wenn D(und deshalb e) ist teilerfremd mit φ(u). In äquivalenter Notation (f(/7), d)=.

Jetzt haben wir alles, um die RSA-Schaltung einzuführen. Die Komponenten der Schaltung sind:

R Und Q- zwei Primzahlen (geheim, ausgewählt);

p - pq(offen, berechnet);

solch e, was (f(i), e)= 1,1 e

D = e l(mod f(/?)) (geheim, berechnet).

Der private Schlüssel besteht aus (d,n), und offen - von (e, p). Nehmen wir an, dass Benutzer A seinen öffentlichen Schlüssel veröffentlicht hat und Benutzer B nun die Nachricht M an ihn weiterleiten wird.

Anschließend berechnet Benutzer B die verschlüsselte Nachricht

Nachdem Benutzer A diesen Chiffretext erhalten hat, entschlüsselt er ihn durch Berechnen

Es ist sinnvoll, hier eine Begründung für diesen Algorithmus anzugeben. Wurden ausgewählt ihr d so dass

Es sieht also scheiße aus kts>(p)+. Aber durch eine Folge des Satzes von Euler, für zwei beliebige solcher Primzahlen R Und qu ganze Zahlen p = pqn M, dassO die Beziehungen erfüllt sind

Deshalb

Jetzt haben wir

Tabelle 10.1 fasst den RSA-Algorithmus zusammen und Abb. Abbildung 10.1 zeigt ein Beispiel für seine Anwendung. In diesem Beispiel werden die Schlüssel wie folgt berechnet:

• 1. Es werden zwei Primzahlen ausgewählt: p- 7 wq- 17.
• 2. Berechnet p =pq= 7 x 17 = 119.
• 3. Berechnen Sie f (p) - (p -)(q - 1) = 96.
• 4. Ausgewählt e, Koprime mit f (P)= 96 und kleiner als f(i); in diesem Fall = 5.
• 5. Dies steht fest D, Was de= 1 (mod 96) und d 96. Der entsprechende Wert wäre d= 77, da 77 x 5 = 385 = 4 x 96 + 1.
• 6. Das Ergebnis ist ein öffentlicher Schlüssel KU = (5, 119) und ein privater Schlüssel KR = (77, 119).

Dieses Beispiel zeigt die Verwendung dieser Schlüssel mit der Klartexteingabe M = 19. Beim Verschlüsseln wird 19 auf die fünfte Potenz erhöht, was 2.476.099 ergibt. Eine Division durch 119 ergibt einen Rest von 66. Daher ist 19 5 = 66 (mod 119). , und daher wird der Chiffriertext 66 sein. Nach der Entschlüsselung stellt sich heraus, dass

Reis. 10.1.

Tabelle 10.1